Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 05. 2010 19:15 — Editoval MiK1234 (03. 05. 2010 21:01)
Hyperbola
Dobrý den, potřeboval bych pomoct s těmito příklady:
I. Sestavte středovou rovnici hyperboly s vrcholem A[2;1], jestliže znáte její asymptoty: as1: x-2y+2=0; as2: x+2y+2=0...
Určete délku tětivy, kterou vytíná na přímce rovnoběžné osou y a procházející ohniskem.
II. Je dána hyperbola 4*(x-2)'2 -y'2 -4=0... V průsečících hyperboly s osou y veďte přímky, které mají s hyperbolou právě jeden společný bod. Přímky zapište obecnými rovnicemi.
Celý den jsem počítal fyziku, proto už mi to na hyperbolu vůbec nemyslí.
Čím detailnější řešení, tím lépe
Předem děkuji za postup a řešení.
Offline
- (téma jako vyřešené označil(a) jelena)
#3 03. 05. 2010 22:21
Re: Hyperbola
↑ MiK1234:
Ten bod A se mi nelíbí. Ale KDYBY ![kopírovat do textarea $A[2;0]$](/mathtex/3f/3f60d44319969eca7149d9edb8643bed.gif) .
.
Průsečík asymptot dává střed ![kopírovat do textarea $S[-2;0]$](/mathtex/93/934e9a88f50cc78183f538c5a15e9959.gif)

Asymptotu můžeme přepsat do tvaru 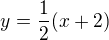 , to znamená, že
, to znamená, že  ,
, 
Rovnice hyperboly 
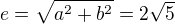
Jedno ohnisko má souřadnice ![kopírovat do textarea $F[-2+2\sqrt5;0]$](/mathtex/9b/9b887acee960f52de56cf21f3cc518e3.gif)
Dosazením za  do rovnice hyperboly
do rovnice hyperboly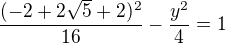

Délka tětivy je 2.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 04. 05. 2010 17:49
Re: Hyperbola
↑ MiK1234:
2)
Průsečíky s osou y = x-ová souřadnice průsečíku = 0
Dosadíme za x = 0 do rovnice hyperboly
Průsečíky jsou: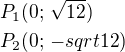
Rovnice přímek procházející průsečíky budou: -dosadíme průsečík P_1 (jeho x-ovou a y-ovou souřadnici a dopočteme q
-dosadíme průsečík P_1 (jeho x-ovou a y-ovou souřadnici a dopočteme q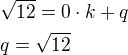
Rovnice přímky bude: -toto dosadíme do rovnice hyperboly
-toto dosadíme do rovnice hyperboly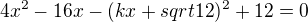 - úpravou dospějeme k rovnici (úpravu si udělej za DÚ - nechce se mi to vypisovat)
- úpravou dospějeme k rovnici (úpravu si udělej za DÚ - nechce se mi to vypisovat)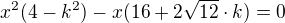 - aby hledaná přímka měla s touto hyperbolu jeden společný bod, pak diskriminant této kvadr. rovnice musí být nula (D=0)
- aby hledaná přímka měla s touto hyperbolu jeden společný bod, pak diskriminant této kvadr. rovnice musí být nula (D=0)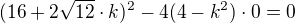 - úpravou:
- úpravou: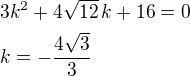
Rovnice přímky bude: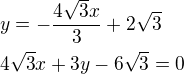
Obdobně pro druhou přímku procházející průsečíkem P_2
Rovnice bude: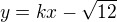
Pokud budeš dobře počítat mělo by Ti vyjít:
Offline