Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 05. 2010 01:34
rovnice hyperboly
zdravím, chtěl bych poprosit o výpočet s rozepsaným postupem, potřebuji si na to napsát opravku:
a) stanovte rovnici hyperboly,, která má ohniska v hlavních vrcholech elipsy  a hlavní vrcholy v ohniscích elipsy
a hlavní vrcholy v ohniscích elipsy
b) určete průsečíky obou křivek
c) napište rovnici tečen v jednom jejich průsečíku
d) vypočtěte odchylku těchto tečen
Offline
- (téma jako vyřešené označil(a) zdenek1)
#2 09. 05. 2010 07:11
Re: rovnice hyperboly
Ahoj, z tohoto jsem už poněkud mimo, ale snad jsem tomu rozuměla a něco mi zůstalo. Takže podle mě je postup následující:
1]
Budeme vycházet z normované středové rovnice pro elipsu: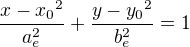
a hyperbolu: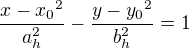
kde ![kopírovat do textarea ${S=[0,0]}$](/mathtex/9e/9e736c3086030b5df8ae15ddbeaf89c8.gif)
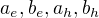
Jsou po řadě hlavní a vedlejší osa elipsy, hlavní a vedlejší osa hyperboly.
Dále platí: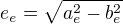
což udává excentricitu, neboli vzdálenost středu od ohniska elipsy. Pro hyperbolu platí malinko odlišný vztah: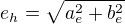
Postupujeme takto:
Nejprve převedeme rovnici elipsy na normovaný středový tvar vydělením rovnice 6 a dostáváme: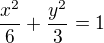
Z této rovnice a vlastností hyperboly a elipsy (viz. např. wikipedie) vyplývá:![kopírovat do textarea ${S_{e}=S_{h}=[0,0]}$](/mathtex/a0/a0cc112b8a736345936cbe22b7ecb433.gif)
neboli střed obou kuželoseček leží v počátku.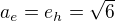
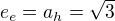
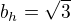
Takže dostaneme rovnici hyperboly: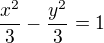
2]
Průsečík obou křivek dostaneme řešením soustavy jejich rovnic, vychází 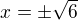 a
a 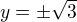
3]
Rovnice tečny hyperboly je zde http://cs.wikipedia.org/wiki/Hyperbola# … .9Bn.C3.AD , stačí dosadit do vzorce, analogicky pro elipsu je rovnice její tečny 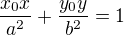 , opět stačí dosadit.
, opět stačí dosadit.
4]
Odchylka dvou přímek např. zde: http://www.aristoteles.cz/matematika/an … rimka.php.
Snad to trochu pomohlo...
Offline