Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 05. 2010 15:48
Stereometrie - přijímačky na VŠ
Zdravím, prosím o radu, mám tu pár úloh ze sbírky k přípravě na přijímací zkoušky na VŠ a nevím si vůbec rady:
1) Obsahy tří stěn kvádru, které mají společný právě jeden vrchol, jsou  . Jaký je objem kvádru?
. Jaký je objem kvádru?
[Správný výsledek má být:  ]
]
2) Kouli o poloměru r je opsán rotační kužel o výšce v=4r. Objem kužele je? [ ]
]
3) Středový úhel kruhové výseče, do které se rozvine plášť rovnostranného rotačního kužele, je? [ ]
]
4) Hrana krychle, která je vepsaná do rotačního rovnostranného kužele s poloměrem podstavy r? [ ]
]
5) Střed koule o poloměru r je vrcholem rotačního kužele, jehož podstava se koule dotýká. Jestliže objemy obou těles jsou stejné, poloměr podstavy kužele je? [2r]
6)Pravidelný trojboký jehlan ABCV je vepsaný do polokoule o poloměru r tak, že jeho podstava ABC je vepsaná hraniènímu kruhu polokoule. Objem jehlanu je? [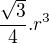 ]
]
7) První ze dvou souosých rotačních kuželů má vrchol ve středu podstavy druhého kužele (a naopak). Poloměry jejich podstav jsou r1, r2. Potom polomìr kružnice, ve které se protínají jejich pláště, je? [ ]
]
Předem děkuji za jakoukoli radu.
Offline
#2 09. 05. 2010 16:03 — Editoval Tychi (09. 05. 2010 16:05)
Re: Stereometrie - přijímačky na VŠ
1. Označ si hrany kvádru a, b, c.
Pak jedna strana má obsah 
druhá 
třetí 
Tebe zajímá objem kvádru, čili  .
.
Stačí se kouknout a vidíš, že když všechny tři obsahy pronásobíš, dostaneš  .
.
Proto objem  .
.
K těm ostatním ..nakresli si obrázek a vyznač, co znáš (obvykle body dotyku a vzdálenosti od nich někam jinam), pak už bys měl vidět jak postupovat.
Vesmír má čas.
Offline
#3 09. 05. 2010 20:37
Re: Stereometrie - přijímačky na VŠ
↑ Tychi: Díky. :-) Já jsem si právě obrázky nakreslil a vše vyznačil. To dělám vždy u těchto úloh, akorát tady to řešení nějak nevidím. Třeba ta dvojka - kdyby ten rotační kužel byl rovnostranný, už bych to měl spočítané. Asi to nebude nic těžkého, ale tady mi nějak dochází nápady. :-(
Offline
#4 09. 05. 2010 20:47
Re: Stereometrie - přijímačky na VŠ
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 09. 05. 2010 21:30
Re: Stereometrie - přijímačky na VŠ
K 6. příkladu. Podstavou je rovnostranný trojúhelník. Pokud v jeho "středu" tam odkud vychází výška do vrcholu nakreslíme spojnice s vrcholy stran, zjistíme, že tyto spojnice jsou dlouhé  . Z vlastností rovnoramenného a rovnostraného trojúhelníka zjistíme, že jsou zde úhly 30° a jeden 120°. Pomocí rozšířené kosinovy věty dopočítáme stranu a. Poté už stačí dosadit do vzorce pro výpočet objemu jehlanu. Pro lepší představu snad napomůže moje řešení.
. Z vlastností rovnoramenného a rovnostraného trojúhelníka zjistíme, že jsou zde úhly 30° a jeden 120°. Pomocí rozšířené kosinovy věty dopočítáme stranu a. Poté už stačí dosadit do vzorce pro výpočet objemu jehlanu. Pro lepší představu snad napomůže moje řešení. 
Opět pokud by měl nějáký matematik návrh lepšího řešení, tak ať poradí.
Offline
#6 19. 04. 2024 11:44
- Mája&Kubík
- Zelenáč
- Příspěvky: 1
- Škola: FSv ČVUT
- Pozice: student
- Reputace: 0
Re: Stereometrie - přijímačky na VŠ
2) Kouli o poloměru r je opsán rotační kužel o výšce v=4r. Objem kužele je? [[mathjax]\frac{8}{3}.\pi . r^3[/mathjax]]
Vyřešit se dá přes podobné trojůhelníky.
Odkaz
Offline
