Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Maximum transcendentní funkce (TOTO TÉMA JE VYŘEŠENÉ)
#2 27. 04. 2010 18:38 — Editoval Pavel (27. 04. 2010 18:40)
Re: Maximum transcendentní funkce
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 28. 04. 2010 10:19 — Editoval Rumburak (28. 04. 2010 11:12)
#5 09. 05. 2010 23:36 — Editoval Marian (09. 05. 2010 23:37)
Re: Maximum transcendentní funkce
Je na čase prozradit i mé řešení. Tady je ...
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Maximum transcendentní funkce (TOTO TÉMA JE VYŘEŠENÉ)

 , přičemž platí vztah
, přičemž platí vztah  . Najděte, jaké největší hodnoty nabývá výraz
. Najděte, jaké největší hodnoty nabývá výraz
 , tzn.
, tzn.  . Pak
. Pak
 a
a  reálná čísla, pak platí
reálná čísla, pak platí ,
,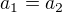 nebo
nebo  .
. . Platí pak buď
. Platí pak buď  , nebo
, nebo 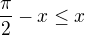 .
.
 , tj.
, tj.  .
. ,
,  ,
, 
 , kde
, kde  .
. ,
,  snadno zjistíme, že funkce G je sudá, proto se v dalším omezíme na
snadno zjistíme, že funkce G je sudá, proto se v dalším omezíme na  .
. .
. pro
pro  klesající s maximem v bodě 0, toto maximum je
klesající s maximem v bodě 0, toto maximum je  .
. ,
,  . Snadno se ověří přímým výpočtem, že druhá derivace funkce
. Snadno se ověří přímým výpočtem, že druhá derivace funkce  je záporná a tudíž konkávní. Jensenova nerovnost v tomto případě říká, že pro kladná čísla
je záporná a tudíž konkávní. Jensenova nerovnost v tomto případě říká, že pro kladná čísla  ,
,  , platí nerovnost
, platí nerovnost
 pro
pro  je vhodně zvolená reálná konstanta. Tato soustava se vyřeší velmi snadno, totiž jejím řešením je aritmetický vektor
je vhodně zvolená reálná konstanta. Tato soustava se vyřeší velmi snadno, totiž jejím řešením je aritmetický vektor  při
při  . Hodnoty
. Hodnoty  pro
pro  a
a  splňující zadání úlohy (dále již nebudu rozlišovat hodnotu složky vektoru příslušející té které neznámé čárkou od označení samotné neznámé). Tedy bude po aplikaci Jensenovy nervnosti
splňující zadání úlohy (dále již nebudu rozlišovat hodnotu složky vektoru příslušející té které neznámé čárkou od označení samotné neznámé). Tedy bude po aplikaci Jensenovy nervnosti

 . Odtud hledaný odhad
. Odtud hledaný odhad 