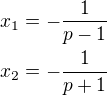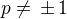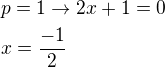Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 12. 05. 2010 13:13 — Editoval Cheop (12. 05. 2010 13:14)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Parametr
↑ Mathe:
Právě když bude 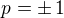 pak to nebude rovnice kvadratická, ale lineární
pak to nebude rovnice kvadratická, ale lineární
Opravdu nevím co po nás tazatel chce. On zřejmě nenapsal celé zadání.
Já to řešil pro takové p, aby to zůstalo rovnicí kvadratickou.
Nikdo není dokonalý
Offline
#5 12. 05. 2010 13:26 — Editoval Mathe (12. 05. 2010 13:28)
Re: Parametr
Parametrické rovnice chápu tak, že za parametr dosazuji libovolné číslo, které mám dovolené. Nevidím tedy důvod, proč bych nemohl za parametr dosadit 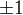 .
.
Napíši zde moje řešení:
A do té rovnice co je jako poslední již dosazuji za parametr libovolné číslo, kromě 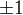 (z podmínek).
(z podmínek).
Offline
#9 12. 05. 2010 13:50 — Editoval Rumburak (12. 05. 2010 14:16)
Re: Parametr
↑ rddior:↑ Mathe: ↑ Cheop:
Součástí řešení rovnic s parametrem by obecně měla být diskuse, při hodnocení (v písemce a pod.) se na tuto formální stránku
klade docela důraz.
V zadání se neříká, má-li tato rovnice být nutně kvadratická, proto je potřeba do diskuse zahrnout i případy, kdy kvadratická není.
Postupoval bych takto [ kolegovi Cheopovi se omlouvám za "zcizení" částí jím napsaného textu :-) ]: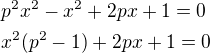
I. Pro 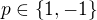 jde o lineární rovnici
jde o lineární rovnici 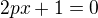 s kořenem
s kořenem 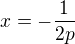 .
.
II. Pro 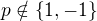 jde o rovnici kvadratickou s diskriminantem
jde o rovnici kvadratickou s diskriminantem  ,
,
která má dva různé reálné kořeny 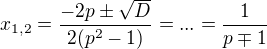 .
.
Offline
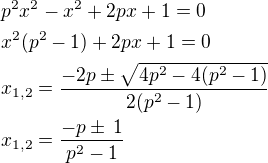 - úpravou:
- úpravou: