Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 06. 2010 17:00
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
exponenciální rovnice 1.
Ahoj, mohl by mi prosím někdo pomoc s tímto příkladem? Výsledek má být 3,ale já nevím jak k tomu mám dojít. Děkuji a za pomoc.
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#3 06. 06. 2010 17:14
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 1.
↑ Sarky:
Děkuji, a kdyby jsi neznal výsledek tak to uděláš jak?
Offline
#4 06. 06. 2010 17:18
Re: exponenciální rovnice 1.
↑ Lucinecka88:
(3/4) na x = 27/64 ptáš se, 3/4 na kolikátou je 27/64. Jinak bych to neveděl.
Offline
#5 06. 06. 2010 17:38
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 1.
↑ Sarky:
Tak takto mi to učitelka neuzná, musím ji napsat nějaký postup.
Offline
#6 06. 06. 2010 17:45
Re: exponenciální rovnice 1.
↑ Lucinecka88:
Musí ti ro uznat, jinak se to řešit nedá.. když tak si můžeš vedle rovnice napsat poznámku 3 na 3= 27 , 4 na 3 = 64
Offline
#7 06. 06. 2010 17:47
Re: exponenciální rovnice 1.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#8 06. 06. 2010 17:47
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 1.
↑ Sarky:
tak uvidím co mi řekne. děkuji
Offline
#11 06. 06. 2010 18:09
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 1.
Ještě bych prosila o pomoc s tímto příkladem děkuji.
Offline
#12 06. 06. 2010 18:18
Offline
#13 06. 06. 2010 18:19
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 1.
↑ jarrro:
Jak jsi to prosím udělal?
Offline
#15 06. 06. 2010 18:26 — Editoval hradecek (06. 06. 2010 18:27)
Re: exponenciální rovnice 1.
↑ Lucinecka88:
použiješ vetu od ↑ easy:
a už by to nemal byť problém :)))...
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#16 06. 06. 2010 19:06
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 1.
Děkuji. Ještě bych potřebovala pomoc s tímto příkladem prosím. Děkuji
Offline
#19 06. 06. 2010 21:11
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 1.
Ahoj, mohl by mě prosím někdo pomoc s tímto příkladem?Děkuji
Offline
#21 07. 06. 2010 09:30 — Editoval Lucinecka88 (07. 06. 2010 09:58)
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 1.
↑ FailED:
Ahoj, děkuji. Jenom bych se chtěla zeptat, kde jsi tam vzal tu 9. Už to vím promin.
Offline

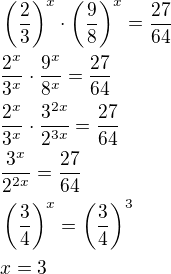
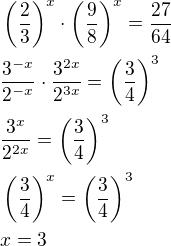
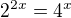
![kopírovat do textarea $\sqrt[n]{a^k} = a^{\frac{k}{n}}$](/mathtex/78/78e1c02f0a2b59845fa2f807d6644506.gif)