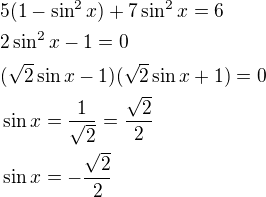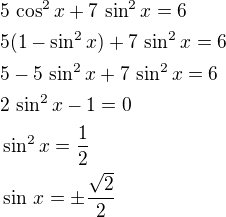Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 06. 2010 16:06
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
goniometrické rovnice 1.
Ahoj, mohl by mě někdo prosím pomoc s pár příklady? Totálně nevím jak to dělat. Předem děkuji.
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#2 08. 06. 2010 16:20
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: goniometrické rovnice 1.
↑ Lucinecka88:
1. cos^2 (x) bych nahradil 1 - sin^2 (x). Pak dostanete rovnici, ve které použijte substituci.
2. sin 2x napište jako 2*sin x*cos x a tg x rozepište jako podíl sin x / cos x a celou rovnici vynásobte cos x.
Tím dostanete sin x * cos x + 2*sin x * cos x = sin x. Pak sin x převedte nalevo a vytkněte sin x.
Offline
#3 08. 06. 2010 16:22
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: goniometrické rovnice 1.
↑ Lucinecka88:
3. cotg x napište jako 1/tg x, rovnici vynásobte tg x a pak použijte opět substituci.
Offline
#4 08. 06. 2010 16:27
Re: goniometrické rovnice 1.
1. použij vzorec sin^2 x+cos^2 x = 1 ------->cos^2 x= 1 - sin^2 x
3. udělej si za tg substituci tg x=a a v tom případě cotg x=1/a
2. sin x + 2cos x sin x - sinx/cosx=0
sin x*( 1 + 2cosx - 1/cosx)=0 ---------> sin x=0 nebo 1 + 2cox - 1/cosx
1 + 2cosx - 1/cosx=0 /*cosx
cosx + 2cos^2 x - 1=0 ------> cos x=1/2 nebo cos x= -1
Offline
#5 08. 06. 2010 18:30
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 1.
Trochu nechápu jak mám udělat tu 1.
Offline
#6 08. 06. 2010 20:09
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 1.
Mohl by mě prosím někdo vysvětlit ty příklady? Děkuji
Offline
#9 09. 06. 2010 09:57
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 1.
U té dvojky, když roznásobuju cosx tak mi vyjde toto: sinx*cosx + 2sinx*cos^2 (x) = sinx
Offline
#10 09. 06. 2010 10:30
Re: goniometrické rovnice 1.
↑ Lucinecka88:
2)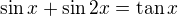
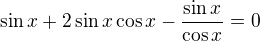
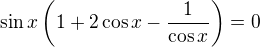
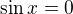 nebo
nebo 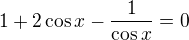
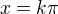 nebo
nebo 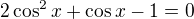
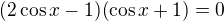
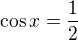 nebo
nebo 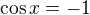
 nebo
nebo 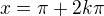
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#12 09. 06. 2010 10:56
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: goniometrické rovnice 1.
↑ Lucinecka88:
Na posledním řádku by mělo být: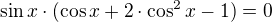
Offline
#13 09. 06. 2010 11:03
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 1.
↑ stepan.machacek:
Děkuji, takže sinx = 0? Závorku dělím na druhou stranu.
Offline
#14 09. 06. 2010 11:04
Offline
#15 09. 06. 2010 11:07
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 1.
↑ zdenek1:
Nechápu to tvoje nebo.
Offline
#16 09. 06. 2010 11:12
Re: goniometrické rovnice 1.
↑ Lucinecka88:
Součin dvou výrazů je nula, když aspoň jeden z nich je nula.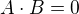 právě tehdy, když
právě tehdy, když  nebo
nebo  .
.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#17 09. 06. 2010 11:38
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 1.
↑ zdenek1:
takže jestli to dobře chápu tak sinx=0 a (cosx+2cos^2x - 1)=0. 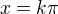 a co znamená toto?
a co znamená toto?
Offline
#18 09. 06. 2010 11:40
#20 09. 06. 2010 12:28
Offline
#21 09. 06. 2010 12:58
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 1.
↑ zdenek1:
Proč 180° místo 360°?
Proč to nemůže být 0°?
Offline
#22 09. 06. 2010 13:02
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: goniometrické rovnice 1.
↑ Lucinecka88:
Řešení je: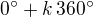 - můžeš vydělit 2 a dostaneš:
- můžeš vydělit 2 a dostaneš: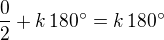
Nikdo není dokonalý
Offline
#23 09. 06. 2010 13:06
Re: goniometrické rovnice 1.
1) protože perioda, kdy je fce sin rovna nule je 180°.
2) protože fce cos je rovna -1 až ve 180°, v nule je rovna 1.
Nezapomeň uvést podmínku 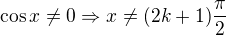
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline