Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Plosny obas casti roviny 5 (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 06. 2010 12:37
Plosny obas casti roviny 5

- tentokrat by som potreboval poratit pri zadavani do wolframalpha, jedna sa mi o x=8 ..... v prikalde 46, a chcel sa spytat dalej ako by sa rucne zistovalo ako dany graf vypada .... lebo prec len na pisomke wolframalpha nemozem pouzit .... jedna sa mi hlavne o take zlozitejsie zapisi ako napr. x=2/(3x^2+5)^2 -1
- pri 47 by som tietz potreboval poradit so zadavanim toho ln .... ked tam napisem ln, ono mi to prehodi na log, graf lnx viem nakreslit, lenze probme je s tym ln^2x
Offline
- (téma jako vyřešené označil(a) johny0222)
#2 10. 06. 2010 17:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
↑ johny0222:
ve wolfram to je tak, jak je zadáno - odkaz.
Jak nakreslit - buď si vyjádřiš y=f(x) a nakresliš. Je třeba dávat pozor na def. obory.
Také se dá docela úspěšně naučit kreslit grafy x=f(y) tak, že otočíš papír o 90 stupňů, nakresliš a potom ten papír otočíš zpět (ale to je spíš pouťový folklor - proto vyžaduje určitý nácvik).
-------------------------------------------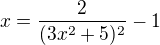 to je rovnice k řešení nebo se to má zakreslit?
to je rovnice k řešení nebo se to má zakreslit?
-------------------------------------------
zadaní 47) pokud umíš nakreslit y=ln(x), tak graf y=(ln(x))^2 vznikne tak, že bod (1, 0) zůstane na místě, čast původního grafu nad osou x bude podobného chování jako původní, jen do hodnoty e na ose x bude pod původní ln(x), potom nad. Původní graf, který je pod osou x na intervalu 0 až 1 (záporné hodnoty funkce) se změní na kladné - daji se naznačit alespoň přibližně). Nás bude zajimat úsek mezi x=1, x=e.
Náznak řešení rovnice 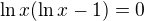 je v pořádku, je to opět součin, tedy řešení je
je v pořádku, je to opět součin, tedy řešení je 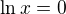 nebo
nebo  . Podařilo se dořešit?
. Podařilo se dořešit?
Offline
#4 10. 06. 2010 19:54
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Plosny obas casti roviny 5
nesmi se integrovat na intervalu od 0 do 1, ale na intervalu od 1 do e, tak jak to pise jelena.
Odkaz
Offline
#5 10. 06. 2010 21:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
↑ kaja(z_hajovny):
zdravím Vás a děkuji za odkaz, ale čím budeme bavit obecenstvo o poutích? Vy budete ručně integrovat (třeba metodou Остроградского), já budu ručně kreslit grafy. Je třeba se zdokonalovat, nebo nás obecenstvo vypiská.
graf som nevdel nakreslit, teda pokusil som sa o to , lenze to nei ohranicene
V předchozích krocích jsme našli 2 průsečíky, tedy víme, na kterém intervalu je ohraničeno. Abychom doladili, která funkce na tomto intervalu je horní a ktera je dolní, vezmeme jednu hodnotu x z intervalu mezi 1 a e a dosadíme do zápisu funkcí. Zvolila jsem na tomto intervalu 2
y= ln(2)=... y=(ln(2))^2=.... která hodnota bude větší, tá funkce bude horní.
x=2/(3x^2+5)^2-1 treba zakreslit, ako sa zistia prisecniky s osou x-ovou, vrchol ...
tak předpokládám, že to jsou 2 funkce:
a) 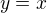 (tu víme zakreslit),
(tu víme zakreslit),
b) 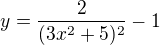 , nejdřív bych si představila funkci
, nejdřív bych si představila funkci 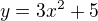 - je to parabola otevřena nahoru s minimální hodnotou "vrcholem (0, 5)". Umocněním takové paraboly na druhou vzníká nová skoroparabola s minimální hodnotou "vrcholem (0, 25)". Když budu 2 dělit hodnotami z paraboly, tak největší hodnoty dosahnu ve vrcholu a bude to bod (0, 2/25), ostatní hodnoty budou symetricky vzhelem k ose y klesat nalevo a napravo od vrcholu a graf se bude přibližovat k ose x. Záporných hodnot nenabývaji. Bude to takový zvon. Nakonec celý ten zvon posunu po ose y dolu o 1.
- je to parabola otevřena nahoru s minimální hodnotou "vrcholem (0, 5)". Umocněním takové paraboly na druhou vzníká nová skoroparabola s minimální hodnotou "vrcholem (0, 25)". Když budu 2 dělit hodnotami z paraboly, tak největší hodnoty dosahnu ve vrcholu a bude to bod (0, 2/25), ostatní hodnoty budou symetricky vzhelem k ose y klesat nalevo a napravo od vrcholu a graf se bude přibližovat k ose x. Záporných hodnot nenabývaji. Bude to takový zvon. Nakonec celý ten zvon posunu po ose y dolu o 1.
Průsečík s osou x je řešení rovnice 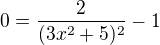 ,
,
Můžeš si to ověřit u stroje, zda mám pravdu. V pořádku?
Offline
#7 11. 06. 2010 10:46 — Editoval kaja(z_hajovny) (11. 06. 2010 10:54)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Plosny obas casti roviny 5
Spatne, bud klikne te na odkaz ve ctvrtem prispevku anebo cekejte, az k Vam dorazi pout :), viz ↑ jelena:
Rada: jak nakreslit y=f(x)^2
1 .nakreslim f(x)
2. co je pod osou x preklopim nahoru
3. nakreslim y=1, body, kde se protne primka s grafem zustanou na miste
4. body nad y=1 se posunou vys, protoze a^2>a pro a>1
5. bodu mezi y=1 a y=0 se posunou niz, portoze a^2<1 pro 0<a<1
6. pripadne hroty na ose x vyhladim do obloucku
7. popremyslim o zakoupeni licence na tento postup a usporadani pripadne snury poutovych vystoupeni :)
Offline
#8 11. 06. 2010 10:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
↑ johny0222:
děkuji, ale chybí označení jednotlivých křívek. Správný graf je v odkazu ↑ kaja(z_hajovny):.
Která z těchto hodnot je tedy větší?
y= ln(2)=...
nebo
y=(ln(2))^2=...
Ovšem tak, jak máš zakreslen graf, tak křívka nakreslena fixem, má tendenci po průsečíku klesat k ose x, což není pravda, ona má růst. Je to spojeno s konvexnosti - konkávnosti na diskutovaném úseku. Je třeba kreslit tak, aby se nezabodavala do osy x.
johny0222 napsal(a):
a co v priapde ze by bolo zadane ln^3x? bolo by to klesanie strmsie ?
v tomto případě je třeba také udělát si jasno s počtem průsečíku - viz řešení rovnice: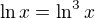
na jednom úseku bude ještě hlubší, potom bude ještě strmější :-)
Děkuji.
Offline
#9 11. 06. 2010 10:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
↑ kaja(z_hajovny):
zdravím Vás :-) tak já ještě budu bavit obecenstvo autorským čtěním svého románu na pokračování. Mám to smazat? Děkuji.
---------------------------------------------------
Úplně OT, ale to si nemohu v debatě s Vámi vynechat - hodná dcera včera obhajovala bakalářku v oboru Anglický jazyk (máte podíl na studijním výsledku, děkuji). Ale celkový závěr ještě není, neb se ještě hodnotí výsledky "bloků státní zkoušky" - tak doplním oficiálně. Milý syn složil postupovou zkoušku na ZUŠ klavir (to mi stalo daleko více nervů, než celé studium hodné dcery :-)
---------------------------------------Konec OT -------------------------------------------------------------------
Offline
#10 11. 06. 2010 10:59
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Plosny obas casti roviny 5
↑ jelena:
Pekny den, nemazal bych to, ja taky kreslim radsi rucne, ale tyhle veci se tezko trenuji pres internet .... Presto jsem se pokusil pridat malou kucharku do sveho prispevku, snad to neni hanebne prozrazeni poutoveho kouzla :)
A velka gratulace hodne dceri i milemu synovi :)
Offline
#11 11. 06. 2010 11:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
↑ kaja(z_hajovny): děkuji i za kuchářku :-)
Já si to představuji tak: - pouť: kolotoče, tam je umelecký kovář a tu truhlář, a co je to tady? - umělecký ruční derivátor - koukejte, dětí, no jaká rarita. A vyděláme si na rozinky (snadno, rychle a veselo - místo vypisování kil papírů na dotace :-)
Kolegovi johny0222 omluva za OT, už může pokračovat v řešení problému.
Offline
#13 12. 06. 2010 09:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
↑ johny0222:
Děkuji.
Jelikož jsme našli hodnoty x pro průsečíky grafů ln(x) a ln^2(x), tak se zaměřujeme na interval od jednoho průsečíku  do druhého průsečíku
do druhého průsečíku 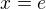 . Ty pořad kresliš někde jinde.
. Ty pořad kresliš někde jinde.
Jak se kreslí - popisuje ↑ kaja(z_hajovny): a já to popisuji ↑ zde: a ↑ zde:
Graf opravdu vypadá takto - viz tento odkaz.
Už je to v pořádku?
Offline
#15 12. 06. 2010 09:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
promiň, ale ten odkaz má ↑ kaja(z_hajovny): ve 4. příspěvku a ještě ho opakujeme různě v textu.
Máš pravdu - my tady s kolegou máme zbytečné (ale radostné OT:-) Ty tady v tématu máš 3 různé problémy k řešení (je třeba si zakladat samostaná témata na každý).
"Ste si fifty-fifty :-)" (c)
Offline
#17 12. 06. 2010 10:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
↑ johny0222:
ve 2. řádku před 2 má být "plus" - je to tak?
Offline
#21 12. 06. 2010 10:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
pro pořádek - * značí násobení. Je to tak?
ja som praveze vychadzal stoho ze e^0=1 a potom ln1= 0
Jakou to má souvislost s dosazování hodnoty x=e do zápisu x*ln(x)?
a co potom v pripade e*ln^2e ? je to to iste ako e*lne ?
jelikož ln(e)=1, tak 1^2=1 a v tomto pripade je výsledek stejný
koniec toho prikladu e*1= 1?
Není.
Co je výsledek příkladu 5*1=.....?
Děkuji.
Offline
#24 12. 06. 2010 14:39 — Editoval jelena (12. 06. 2010 18:14)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obas casti roviny 5
↑ johny0222:
K zadání 46)
je potřeba pozorně zakreslit celé zadání - průsečík křívek, myslím nebude podstatný, jelikož omezení je pomocí y=1, y=6.
Jinak průsečík se lépe počíta ze zápisu ![kopírovat do textarea $\frac14y^2=8\sqrt[3]y$](/mathtex/25/25adee45dd9c7aae18cffdbe5ab25944.gif) , odsud y, potom dopočet x. Zkus jen pro kontrolu, zda je mimo zadanou oblast pro výpočet obsahu.
, odsud y, potom dopočet x. Zkus jen pro kontrolu, zda je mimo zadanou oblast pro výpočet obsahu.
Takové hodnoty y (y=1 a y=6) je potřeba dosadit do jednotlivých funkci y=f(x) a najit odpovídající x.
Bude jasno, na kterém intervalu je jako horní funkce jedna ze zadaných křívek a jako dolní funikce je jedna z přímek y=1.
Na dalším intervalu naopak - horní funkce je přímka y=6, dolní je jedna ze zadaných křívek.
Dálo by se také integrovat tak, jak je zadáno po dy, ale myslím, že by to stalo jen za pokus (cvičně).
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Plosny obas casti roviny 5 (TOTO TÉMA JE VYŘEŠENÉ)





