Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 06. 2010 23:08
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Ještě jedna řada
Prosím o pomoc ještě s jednou řadou... 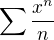 spočítal jsem si nutnou podmínku a vyšlo mi
spočítal jsem si nutnou podmínku a vyšlo mi  (BTW musim vzdycky tu NPK pocitat?) No ale nevim co dál... když použiju odmocninové kriterium dostanu limitu z x.. a to mi asi moc nepomuze... tak jsem zkusil podilove a vyslo mi
(BTW musim vzdycky tu NPK pocitat?) No ale nevim co dál... když použiju odmocninové kriterium dostanu limitu z x.. a to mi asi moc nepomuze... tak jsem zkusil podilove a vyslo mi  Nu a nevim co dál... Napadlo mě jetli se to teda nedělá tak, že vemu ten interval z nutný podmínky a nějak ho zkouším aplikovat na to co mi vyslo v tom kriteriu.. ale nevim moc.. spis mozna neznam obecně ten postup... kdyz by ste byl nekdo tak hodny:-)
Nu a nevim co dál... Napadlo mě jetli se to teda nedělá tak, že vemu ten interval z nutný podmínky a nějak ho zkouším aplikovat na to co mi vyslo v tom kriteriu.. ale nevim moc.. spis mozna neznam obecně ten postup... kdyz by ste byl nekdo tak hodny:-)
Offline
- (téma jako vyřešené označil(a) ondrej.hav)
#2 14. 06. 2010 23:31 — Editoval Olin (14. 06. 2010 23:33)
Re: Ještě jedna řada
A co říkají ta kritéria? Třeba to limitní odmocninové:
Nechť je  řada. Pokud je
řada. Pokud je ![kopírovat do textarea $\lim_{n \to \infty} \sqrt[n]{|a_n|} \, < \, 1$](/mathtex/ac/acd7fa032c598be103eb66b6ec489324.gif) , tak řada absolutně konverguje. Pokud je
, tak řada absolutně konverguje. Pokud je ![kopírovat do textarea $\lim_{n \to \infty} \sqrt[n]{|a_n|} \, > \, 1$](/mathtex/94/942a4c8eece6bc083d9778669ba2f437.gif) , tak řada diverguje.
, tak řada diverguje.
Aplikací na  dostaneme, že řada absolutně konverguje, pokud je
dostaneme, že řada absolutně konverguje, pokud je  , a diverguje pro
, a diverguje pro  . Případy, kdy
. Případy, kdy  se musí vyšetřit zvlášť.
se musí vyšetřit zvlášť.
Offline
#3 14. 06. 2010 23:42 — Editoval ondrej.hav (14. 06. 2010 23:54)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Ještě jedna řada
↑ ondrej.hav:No jo, ale já pořád nevím proč tam můžu použít to s tou odmocninou? Tu absolutní konvergenci... BTW jak ty případy ověřím??? Ty v 1 a -1???
Je to tak, že tam dosadím ty krajní body a zkoumám jestli ta řada potom konverguje/diverguje?
Offline
#4 15. 06. 2010 01:09 — Editoval Oxyd (15. 06. 2010 01:12)
Re: Ještě jedna řada
Použít to můžeš, protože taková je formulace odmocninového kriteria.
Důkaz toho kriteria ani není tak složitý. Nechť tedy ![kopírovat do textarea $ \lim_{n \to \infty} \sqrt[n]{\left|a_n\right|} = q < 1$](/mathtex/9c/9c42ac8904e383033aa3c41019331e2d.gif) . Vezměme r takové, že
. Vezměme r takové, že  . Protože členy
. Protože členy ![kopírovat do textarea $\sqrt[n]{\left|a_n\right|}$](/mathtex/f6/f6e5380c24c2ffd718cc7b7e402789a6.gif) jdou ke q, které je pod jedničkou, tak existuje nějaké
jdou ke q, které je pod jedničkou, tak existuje nějaké  , že
, že ![kopírovat do textarea $n > n_0 \Rightarrow \sqrt[n]{\left|a_n\right|} < r$](/mathtex/fe/fea2ebd264a820062f512501e0c3e285.gif) . (Jinak by všechny členy byly nad r a nemohly by se libovolně přiblížit ke q.)
. (Jinak by všechny členy byly nad r a nemohly by se libovolně přiblížit ke q.)
Umocněním na n dostáváme  . To znamená, že nekonečně mnoho členů řady
. To znamená, že nekonečně mnoho členů řady  , n_0 počínaje, je menších než členy řady
, n_0 počínaje, je menších než členy řady  -- to je geometrická řada a o odstavec výš jsem řekl, že vezmeme
-- to je geometrická řada a o odstavec výš jsem řekl, že vezmeme  , tedy tahle geom. řada konverguje. Ze srovnávacího kriteria pak máme, že i
, tedy tahle geom. řada konverguje. Ze srovnávacího kriteria pak máme, že i  konverguje.
konverguje.
Praktická aplikace na tvuj příklad: ![kopírovat do textarea $\lim_{n \to \infty} \sqrt[n]{\left|\frac{x^n}{n}\right|} = \lim_{n \to \infty} \frac{\left|x\right|}{\sqrt[n]{n}}$](/mathtex/59/59c1f35e0095b1823ad3033ac0847886.gif) . Víme, že
. Víme, že ![kopírovat do textarea $\lim \sqrt[n]{n} = 1$](/mathtex/4e/4eda7facbbbf2dc0216b7c4bb7144b70.gif) , tedy
, tedy ![kopírovat do textarea $\lim_{n \to \infty} \frac{\left|x\right|}{\sqrt[n]{n}} = \lim \left|x\right| = \left|x\right|$](/mathtex/3a/3a53175d9bb2e1e83df2b5033ef04dd7.gif) . Takže pokud je -1 < x < 1, pak z odmocninového kriteria řada konverguje.
. Takže pokud je -1 < x < 1, pak z odmocninového kriteria řada konverguje.
No a ty zbývající dva případy, x = +1 a x = -1, vyřešíš prostě tak, že to tam dosadíš. Pro x = 1 dostaneš  . Tuhle řadu bys mohl znát.
. Tuhle řadu bys mohl znát.
A ještě k předchozí otázce -- nutnou podmínku konvergence nemusíš vyšetřovat vždy. Máš vyšetřit konvergenci řady -- libovolným způsobem. NPK je jednoduchý nástroj, jak odbýt "očividně divergentní" řadu. Pokud zjistíš, že řada konverguje, tak už nutně NPK platí a vyšetřovat ji nemusíš.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#5 15. 06. 2010 10:31 — Editoval Rumburak (15. 06. 2010 10:35)
Re: Ještě jedna řada
↑ ondrej.hav:
Když se na nějaké úloze zadrhnu, pak mi do budoucna pomůže, pokud si uvědomím, proč se tak stalo.
Tvůj případ zde byl ten, že sis nevěděl rady s limitami
(1) ![kopírovat do textarea $A\,:=\,\lim_{n \to \infty} \sqrt[n]{|a_n|}\,=\,\lim_{n \to \infty} \sqrt[n]{\|\frac{x^n}{n}\|}$](/mathtex/b4/b4e9a956a1e5753f10ef6afcfad64f8f.gif) (Cauchyho kriterium),
(Cauchyho kriterium),
(2) 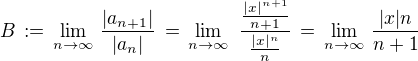 (d'Alembertovo kriterium).
(d'Alembertovo kriterium).
Řešení úlohy pomocí limity (1) Ti vysvětlili kolegové.
Avšak výpočet limity (2) rovněž vede k cíli: a dále jako u kolegů.
a dále jako u kolegů.
Offline
#6 15. 06. 2010 13:54 — Editoval ondrej.hav (15. 06. 2010 14:08)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Ještě jedna řada
↑ Rumburak:Jo, už to relativně chápu. Co když mám ale třeba ještě  Tam by se mělo podle řešení použít integrální kritérium a leibnitzovo... a přesne je tam napsano
Tam by se mělo podle řešení použít integrální kritérium a leibnitzovo... a přesne je tam napsano  (integrální kritérium pro
(integrální kritérium pro  , Leibnizovo kritérium pro
, Leibnizovo kritérium pro  . Tak u toho si vubec nevm rady... To muzu pouzivat na nejaky interval jedno kriterium a na druhy interval jine kriterium?
. Tak u toho si vubec nevm rady... To muzu pouzivat na nejaky interval jedno kriterium a na druhy interval jine kriterium?
EDIT: Nebo jinak... Kdyz dostanu takovyhle (jakykoli) priklad.. JAk postupuju??? To se na to podivam a mel bych poznat automaticky an jakych intervalech to mam resit a jakyma kriteriama?
Offline
#7 15. 06. 2010 14:19
Re: Ještě jedna řada
Oxyd napsal(a):
Použít to můžeš, protože taková je formulace odmocninového kriteria.
...
Umocněním na n dostáváme. To znamená, že nekonečně mnoho členů řady
, n_0 počínaje, je menších než členy řady
-- to je geometrická řada a o odstavec výš jsem řekl, že vezmeme
, tedy tahle geom. řada konverguje. Ze srovnávacího kriteria pak máme, že i
konverguje.
...
Tahle formulace není přesná. Nekonečno ještě vůbec neznamená všechny. Formálně a velmi zjednodušeně, pokud z nekonečné bodové množiny odeberu nekonečně mnoho prvků této množiny, nemusím ještě dostat konečnou bodouvou množinu. Asi jsi chtěl napsat všechny členy od jistého  počínaje.
počínaje.
Upozorňuji také na výhodný Rumburakův postup. Na druhou stranu je odmocninové kritérium silnější než podílové. Konečně bych však chtěl upozornit i na obecnější tvary těchto kritérií obsahující pojem limes superior.
Offline
#8 15. 06. 2010 14:30
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Ještě jedna řada
↑ Marian:A co přsně znamená, že je nějaké kritérium silnější?
Offline
#9 15. 06. 2010 14:43
Re: Ještě jedna řada
↑ ondrej.hav:
Na vyšetření "běžné" (neabsolutní) konvergence u řady  stačí Leibnizovo kritérium a nutná podmínka konvergence (pro záporná x konverguje, jinak diverguje). Pokud chceme vyšetřit i absolutní konvergenci, je třeba nasadit jiné nástroje, třeba integrální kritérium.
stačí Leibnizovo kritérium a nutná podmínka konvergence (pro záporná x konverguje, jinak diverguje). Pokud chceme vyšetřit i absolutní konvergenci, je třeba nasadit jiné nástroje, třeba integrální kritérium.
Některá kritéria vyšetřují pouze absolutní konvergenci (neboli řady s nezápornými členy) - to jsou třeba Cauchyho odmocninové, d'Alembertovo podílové, srovnávací, integrální atd. Pro neabsolutní konvergenci jsou pak Leibnizovo, Abelovo, Dirichletovo… Rozhodnout, jaká kritéria použít, je záležitostí asi hlavně zkušeností, ale existují na to i přibližné "návody" - třeba tento.
To, že je nějaké kritérium A silnější než kritérium B, znamená, že kritérium A dokáže rozhodnout o konvergenci/divergenci všech řad, o kterých lze rozhodnout i pomocí B, ale existují i řady, které A rozhodne a B nikoliv. Toto není zcela formální definice, ale pojem "silnější kritérium" je taky spíše neformální.
Offline
#10 15. 06. 2010 14:56
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Ještě jedna řada
↑ Olin:Ahaaaa... takze kdyz nektera kriteria vysetruji pouze absolutni konvergenci tak tam muzu dat tu absolutní hodnotu žejo? Protozě stejně vyšetřuju jenom ty kladné členy? A díky za objasnění pojmu "silnější"
Offline
#12 15. 06. 2010 15:42
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Ještě jedna řada
↑ Olin:btw. jak spočtu tu řadu pomocí toho kritéria leibnitzova? To si řeknu, že ta řada je klesající pro záporná x? a pak udělám limitu zjiatim ze je nula... takze muzu rovnou rict ze to konverguje na (-\infty; 0)??? ale nevim jestli absolutně??? a když bych chtěl i absolutní, tak bych musel použít integrální... Je to tak?
Offline
#13 15. 06. 2010 16:09 — Editoval Rumburak (15. 06. 2010 17:11)
Re: Ještě jedna řada
↑ ondrej.hav:
Pro určitý přehled uvedu několik všeobecných informací.
Základní kategorií konvergenčních kriterií jsou kriteria srovnávací, kdy vyšetřovanou řadu porovnáváme podle vhodně zvolených hledisek
s některou jinou řadou, o jejíž konvergenci resp. divergenci již máme předem jasno (případně s integrálem u integrálního kriteria). Speciálními
volbami takové "testovací" řady vznikla kriteria další, například i d'Alembertovo a Cauchyovo , kdy zkoumaná řada je de facto porovnávána
s řadou geometrickou, což pochopíš, když si prostuduješ důkazy příslušných vět. Poznat, které kriterium se kdy hodí, je věcí znalostí těch kriterií
a určité zkušenosti získané praxí.
Řada může být navíc libovolně složitá , předpis pro obecný člen se třeba může i větvit podle vlastností konkretního indexu - například  ,
,
kde z(n) je zbytek při celočíselném dělení n : 3 .
Podle toho by se pak musela úloha rozpitvat - třebas rozložením na součet tří řad s tím, že pro různé tyto dílčí řady by mohlo být výhodné použít
různých kriterií.
Dále je podstatný rozdíl mezi konvergencí absolutní a neabsolutní, která je jemnějším jevem a proto vyžaduje i jemnější metodiku.
Offline
#14 15. 06. 2010 16:15
Re: Ještě jedna řada
↑ halogan:
Je ovšem otázka, co se kde bere jako známé. Na školách, kde se nejprve probírají integrály a až pak řady, je možné, že se konvergence těchto řad dokazuje pomocí integrálního kritéria.
↑ ondrej.hav:
Ano, pro Leibnizovo kritérium stačí říct, že jsou členy řady klesající a jdou k nule. O absolutní konvergenci neříká nic, takže se použije to integrální.
Offline
#15 15. 06. 2010 16:49 — Editoval Rumburak (15. 06. 2010 16:58)
Re: Ještě jedna řada
↑ ondrej.hav:
I. Integrální kriterium použijeme na řadu
(1)  ,
,
její konvergence vyjde pro x < -1, v ostatních případech nastává divergence.
II.A. Pro x < -1 pak automaticky je konvergentní i řada
(2)  ,
,
a to vzhledem k předchozímu výsledku - řada (2) je zde tedy absolutně konvergentní.
B. Pro x >= -1 v řadě (2) určitě nenastane absolutní konvergence (opět vzhledem k I), ale mohla by nastat konvergence neabsolutní
(neboť znaménka členů alternují). Leibnizovo kriterium pro takovou konvergenci požaduje, aby pro pevně zvolené x platilo
(a) posloupnost  je monotonní,
je monotonní,
(b)  .
.
Tvrzení (a) je splněno pro každé x,
Tvrzení (b) je splněno právě tehdy, je-li x < 0 .
Za předpokladu, že -1 <= x < 0 , tedy nastává neabsolutní konvergence ředy (2) ,
pro x >= 0 však není splněno tvrzení (b), tedy není splněno ani  , což je nutná podmíka konvergence řady (2),
, což je nutná podmíka konvergence řady (2),
takže v tomto případě řada (2) nekonverguje (ani neabsolutně a tím spíše ani absolutně).
Offline
#16 15. 06. 2010 16:54
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Ještě jedna řada
↑ Rumburak:Jupí.. děkuji... teď už snad vím jak na to :-D
Offline

