Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 06. 2010 17:15
- timebuster
- Zelenáč
- Příspěvky: 5
- Reputace: 0
Pomoc se vzorem
R . sin r = -0.77
R . cos r = 1.63
jak dopočítat R a r???
Offline
- (téma jako vyřešené označil(a) Olin)
#5 23. 06. 2010 18:04
Re: Pomoc se vzorem
↑ b.r.o.z1:
V podstatě jsi udělal to, co jsem navrhoval - to bylo .
.
R můžeme zjistit snadno tak, že obě rovnice umocníme na druhou a sečteme.
Offline
#7 23. 06. 2010 18:06
- timebuster
- Zelenáč
- Příspěvky: 5
- Reputace: 0
Re: Pomoc se vzorem
děkuji, takhle to bude jistě dobře - zkouška funguje na obě rovnice
Offline
#8 23. 06. 2010 18:11
Re: Pomoc se vzorem
↑ timebuster:
v pořádku, rádi jsme ti s olinem pomohli:-)
"Vím, že nic nevím." Sokrates
Offline


 =>
=> 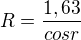 dosadim do první
dosadim do první
 <=
<=




 => přibližně 0,77 => mělo by to být správně
=> přibližně 0,77 => mělo by to být správně