Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dotycnica grafu funkcie (TOTO TÉMA JE VYŘEŠENÉ)
#2 12. 06. 2010 20:07
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: dotycnica grafu funkcie
musi se vzdy dosadit do rovnice tecny nebo normaly. K tomu je potreba jeden bod a dsmernice (u tecny derivace)
Offline
#4 12. 06. 2010 20:49
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: dotycnica grafu funkcie
Ja po ruce nic nemam, ale neni to vubec tezke. A myslim ze lepsi nez cekat, nez nekdo da odkaz na reseny priklad, je vygooglit si neco, nebo neco najit ve sbirkach resenych prikladu v knihovne.
Offline
#5 15. 06. 2010 17:34
Re: dotycnica grafu funkcie
trosku som sa posprtal v nejakych materialoch .... a nakonieco my vyslo toto 
- doplnil som tam aj rovnicu dotycnice, aj ked to tam v zadani nieje
- zarazilo ma len to x=sqrt(2t+1) nevedel som co mam s tym robit .... prislo mi to tam ako zbytocne zadane, potreboval by som nenaku radu ako to tam do toho vypoctu zapasovat, co s tym treba urobit, co to vlastne prectavuje ......
Offline
#6 15. 06. 2010 23:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: dotycnica grafu funkcie
↑ johny0222:
Zdravím,
to asi nebude v pořádku. Křívky jsou zadany parametricky, tedy jak x, tak y se má derivovat po t.
Do výsledku derivace x´(t), y´(t) (pro výpočet směrnice v bodě T) se má dosazovat t, které vypočteme dosazením hodnoty x ze zadaného bodu do zápisu x=f(t) a y=g(t), má se zvolit stejné t, pokud je více kořenů (zde vychází jen jeden).
Případně materiál.
Offline
#8 16. 06. 2010 19:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: dotycnica grafu funkcie
↑ johny0222:
Nebyl by náhled na vaše teoretické materiály? Děkuji.
Vyšlo, že 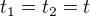 . Tak bych to zhodnotila, že v tomto bodě máme pouze jeden parametr t, tedy je to bod regulární a bude jedna tečná (jednoznačná).
. Tak bych to zhodnotila, že v tomto bodě máme pouze jeden parametr t, tedy je to bod regulární a bude jedna tečná (jednoznačná).
Kdyby to nevyšlo stejné, tak nastupuji různé varianty, jak takový bod pojimenovat (úzel, hrot, vrat...) a podle toho různé varianty jak jsou umístěny tečny.
Ovšem teď jsem se divala na Wikipedii a nějak se mi nezdá zápis věty hned na úvod po názvu Singularita. Nebo to 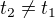 je tak divně vypíchnuto.
je tak divně vypíchnuto.
Kdyby se na to, prosím, podíval někdo z matematických autorit nebo pokud máte nějaký jiný odkaz, děkuji.
Offline
#9 16. 06. 2010 20:12
#10 16. 06. 2010 21:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: dotycnica grafu funkcie
↑ kaja(z_hajovny):
Zdravím Vás a děkuji,
pokud doporučujete, tak to bude určitě stačit (v textu, pravda, moc písmenek, indexů a pomocných označení...)
Kolega Johny totiž ještě ani jednou nedoderivoval x, y (aby mohl použit vzorec z Wikipedie) - tak nevím, jestli třeba v materiálech nemá nějaké povinné kroky, co musí ověřovat - že parametr je jen jeden atd.
A je to tedy tak, že až doderivuje a použije vzorec z Wikipedie, tak za použití souřadnice bodu A dopočte paramatr t a ten dosadí do výsledku derivace? Nebo jinak?
Také ten text ve Wikipediise mi nezdá.
Já Vám kolegu s důvěrou přenechám (sice jsem zaregistrovala, že opět připravujete transformační proces), ale kdybyste měl jasnou představu, jak to chcete, tak bude pátek, přivolá se Super-Admirátor....
Offline
#11 16. 06. 2010 21:24 — Editoval kaja(z_hajovny) (16. 06. 2010 21:28)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: dotycnica grafu funkcie
jelena napsal(a):
↑ kaja(z_hajovny):
A je to tedy tak, že až doderivuje a použije vzorec z Wikipedie, tak za použití souřadnice bodu A dopočte paramatr t a ten dosadí do výsledku derivace? Nebo jinak?
ano ano
po zderivovani a vydeleni vyjde -3*sqrt(2*t + 1)/(t + 2)^2
staci dosadit t=4 a mame k.
na a kdyz mame smernici a bod, tak napsani primky je hracka, nize pripojim, jak jsem to spachal v Sage
Také ten text ve Wikipediise mi nezdá.
Me se take moc nezda, ale je to jenom Wikipedie a navic pojem "neco je singularni" je v matematice tak proflaknuty, ze rozlisovat co presne se mysli tim "byt singularni" bez podrobneho komentare kolem je dost tezke. Proste se to pouziva v prilis mnoha kontextech. A podle te wikipedie by kazda periodicka krivka (napr. kruznice) mela vsechny body singularni coz myslim nesedi na to, ze "singularita" znamena vetsinou nejakou prisernost nebo problemy.
Code:
sage: t=var('t')
sage: x(t)=sqrt(2*t+1)
sage: y(t)=(1-t)/(2+t)
sage: k(t)=factor(diff(y,t)/diff(x,t))
sage: k
t |--> -3*sqrt(2*t + 1)/(t + 2)^2
sage: (k(4),x(4),y(4))
(-1/4, 3, -1/2)
sage: tecna(t)=-1/4*(t-3)-1/2
sage: parametric_plot((x(t),y(t)),(t,0,10))+point((3,-1/2),color='red')+plot(tecna(x=t),(t,1,4),color='green')
rovnice tecny je y=-1/4*(x-3)-1/2
Offline
#13 17. 06. 2010 08:08
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: dotycnica grafu funkcie
johny0222 napsal(a):
- co ste spominaly tie varianty, v priapde ze by to nevyslo rovnake, ake by sa tam teda pouzili ?
??? jake varianty, kde ???
Offline
#14 17. 06. 2010 08:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: dotycnica grafu funkcie
↑ kaja(z_hajovny):
Zdravím Vás a děkuji za celé vysvětlení.
To jsou pravě varianty singularit, kdy vychází různá t (myslím, když křívkyjsou zadany třeba nějak "kvadraticky" snad).
Děkuji.
Offline
#15 17. 06. 2010 08:26 — Editoval kaja(z_hajovny) (17. 06. 2010 08:27)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: dotycnica grafu funkcie
No ja myslim, ze kdyz tam bude treba vznikat smycka, tak v tom bode, kde se to krizi (vyjdou dva parametry t), jsou dve tecny a vyjdou nam obe. Te "singularity" by se totiz dalo zbavit tak, ze dostatecne orezu interval pro t a pak je to prevedene na regularni pripad. Pro derivaci funkce dane parametricky je potreba, aby derivace x podle t nebyla nula, to nam uplne staci.
Code:
sage: t=var('t')
sage: x(t)=(sin(pi*t))
sage: y(t)=(t-t^3)
sage: k(t)=factor(diff(y,t)/diff(x,t))
sage: k
t |--> -(3*t^2 - 1)/(pi*cos(pi*t))
sage: (k(0),x(0),y(0))
(1/pi, 0, 0)
sage: tecna(t)=1/pi*(t-0)-0
sage: (k(1),x(1),y(1))
(2/pi, 0, 0)
sage: tecna2(t)=2/pi*(t-0)-0
sage: parametric_plot((x(t),y(t)),(t,0,1))+\
... point((x(0),y(0)),color='red')+\
... plot(tecna(t),(t,0,1),color='green')+\
... plot(tecna2(t),(t,0,1),color='red')
Offline
#16 19. 06. 2010 00:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: dotycnica grafu funkcie
↑ kaja(z_hajovny):
Děkuji, kolega se neozývá s nějakým námětem.
Tady mám celkem jednoduchou záležitost - příklad 9a) - a v zadaném bodě mám celkem 3 parametry:
t=1 (z obou rovnic) - ten bych použila podle svého pravidla,
t=2 - ten nevezmu, jelikož derivace x po t je nulová.
t=3 (a to nevím, jak zdůvodním, že se nepoužije), navíc ani na obrázkunevidím žádné zdůvodnění.
Také je možné, že neumím řešit kvadratické rovnice.
Nijak to nehoří, já už stejně skoro nedoučuji (a nic takového se v regionu nepožadovalo).
Zdravím Vás.
Offline
#17 19. 06. 2010 12:41 — Editoval kaja(z_hajovny) (19. 06. 2010 12:43)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: dotycnica grafu funkcie
Pekny den, zdravim a dekuji za namet.
Nevim jestli jsem neco nepochopil , ale zda se mi, ze krivka 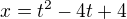 ,
, 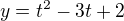 dava pro
dava pro 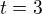 bod [1,2]. Nas vsak zajima bod [1,0]. Soustava
bod [1,2]. Nas vsak zajima bod [1,0]. Soustava  ,
, 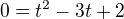 ma jedine reseni,
ma jedine reseni,  .
.
Offline
#18 19. 06. 2010 13:48
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: dotycnica grafu funkcie
↑ kaja(z_hajovny):
Děkuji :-) kvadratické rovnice umím, jen soustavy kvadratických rovnic neumím (přesně řečeno, neumím to správně pojmenovat, co dělám).
To už asi nemám šanci na jarmark v říjnu? - a jsem si secvičila takovou vhodnou jazykovou variantu. Jistě ocenite smysl pro humor od stroje a mějte se pěkně :-)
Offline
#20 24. 06. 2010 10:56
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: dotycnica grafu funkcie
ne ne, to je ohuzel uplne z cesty :(
vlastne jste zacal hledat prusecik primky a krivky, potom jste nesmyslne napsal nejakou kvadratickou rovnici a ziskal jakysi podivny bod  . Je nutno premyslet, co se ma delat.
. Je nutno premyslet, co se ma delat.
je potreba zjistit, pro ktera t je derivace rovna -8/3
Offline
#22 24. 06. 2010 13:34 — Editoval kaja(z_hajovny) (24. 06. 2010 13:35)
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: dotycnica grafu funkcie
Oops, spatne jsem si to precetl, mluvi se o normale, takze derivace ma byt 3/8.
musim urcite smernici te primky co je zadana a potom kolmy smer. a to proto, ze se to pozaduje v zadani.
kde se vzala ta rovnice 8t^3-5t^ .... ? nahodne dosazeni neceho nekam? :)
vzorec pro derivaci funkce dane parametricky je v predchozich prispevcich tohoto vlakna
Offline
#23 24. 06. 2010 17:53
Re: dotycnica grafu funkcie
no oki takze 3/8 ..... lenze odkial sme tam dostali tie 3/8 ? z akeho vypoctu, alebo teda z akej derivacie?
8t^3-5t^ .... sme tam dostali tak ze sme si dosadili x=t^3-t^2 , y=t^2-t-2 do rovnice tej priamky
ako teda urcime tu smernicu priamky? a ten kolmy smer?
a poprosil by som teda jednoznacne vysvetlit co mam urobit, a ked sa teda vysvetluju niektore casti v hadankach, tak by bolo dobre si na tu hadanku aj odpovedat
nemam zas taky dobry prehlad v matike, ale jednoznacna a zrozumitelna odpovet pre tych, ktory sa moc matike nerobumeju, by mi urcite postacila
riesit tieto prikady od nikoho nevyzadujem, to je uz moja starost
Offline
#24 24. 06. 2010 18:00
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: dotycnica grafu funkcie
tecna musi byt kolma k te zadane primce, tj. rovnobezna s normalou. smernice normaly se urci podle poucek z analyticke geometrie.
jak jsem psal, je potreba najit bod, kde je pozadovan derivace. Neni nutne hledat pruseciky a dosazovat jednu rovnici do druhe, protoze s pruseciky se tu nepracuje.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dotycnica grafu funkcie (TOTO TÉMA JE VYŘEŠENÉ)




