Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vztahy mezi kořeny a koeficienty kvadratické rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 06. 2010 15:46
Vztahy mezi kořeny a koeficienty kvadratické rovnice
Nemůžu za žádnou cenu přijít na tyto příklady:
1) Určete všechny hodnoty absolutního členu "q" e R tak, aby jeden kořen kvadratické rovnice 4x^2 - 15x + q = 0 byl druhou mocninou druhého kořene. Výsledek: q_1 = -125/2 , q_2 = 27/2.
2) Aniž rovnici x^2 + 2x + 5 = 0 řešíte, určete součet druhých mocnin jejích kořenů. Výsledek: -6
- v knize je napsán postup x_1^2 + x_2^2 = (x_1 + x_2)^2 - 2*x_1*x_2, kterej jsem ale nepochopil: podle mých znalostí a^2 + b^2 v R rozložit nejde, tak co to je za vzorec? Nechápu ho..Nebo jestli je to nějaký jiný řešení, fakt nevim..
3) Aniž rovnici 5x^2 + 8x + 5 = 0 řešíte, sestavte všechny kvadratické rovnice, jejichž kořeny jsou čísla:
a) třikrát větší než kořeny původní rovnice
b) o tři větší než kořeny původní rovnice
Výsledek:
a) k(5x^2 + 24x + 45) = 0
b) k(5x^2 - 22x + 26) = 0
Díky za odpověď
Offline
- (téma jako vyřešené označil(a) atomic)
#2 24. 06. 2010 16:38 — Editoval zdenek1 (24. 06. 2010 16:39)
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
↑ b.r.o.z1:
2.
Upřesnění:
Edit: Tak sorry, už jsi to tam dal. :-)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 24. 06. 2010 17:19 — Editoval b.r.o.z1 (24. 06. 2010 18:38)
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
1) Využiješ Vietovy vzorce: 


 =je neznama treba y
=je neznama treba y
Z 1. Vietova vzorce:


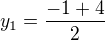



Z 2. Vietova vzorce(vyšla 2 y => 2 q)
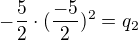

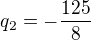
pzn. jelikožjsem předtim nahoře vytkl 4, teď to musim vrátit
=> 

pzn.  a
a  jsou konecne hodnoty q, po kterém se pídíme
jsou konecne hodnoty q, po kterém se pídíme
2) Pzn: 
Opět využiješ Vietovy vzorce:


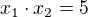
my hledáme m, pro které platí: 
upravíme: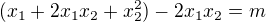

dosadíme z V. vzorců pro danou rovnici výše
3)Zase příklad na Vietovy vzorce
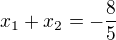

a) hledáme 3krát větší kořeny => nová rovnice bude vypadat:(velkým písmenem značuju hodnoty pro novou rovnici - 

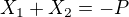










=> nová rovnice je:  po úpravě:
po úpravě: 
b) hledáme kořeny o 3 větší => nová rovnice bude vypadat:(velkým písmenem značuju hodnoty pro novou rovnici - 

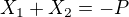

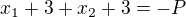




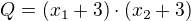




=> nová rovnice je:  po úpravě:
po úpravě: 
"Vím, že nic nevím." Sokrates
Offline
#4 24. 06. 2010 17:20
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
↑ b.r.o.z1:
Kdyby byly nějaké dotazy neboj se zeptat:-D Fuj to byla fuška to sem použitím TeXu dostat:-D
"Vím, že nic nevím." Sokrates
Offline
#5 24. 06. 2010 17:29
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
↑ BrozekP:
díky za tvůj typ :-)
je to správně aspoň?:-D
"Vím, že nic nevím." Sokrates
Offline
#6 24. 06. 2010 17:49
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
↑ b.r.o.z1:
3a nemáš dobře. Pak tam používáš q v jiném smyslu než je v zadání, to není vhodné. (Dokonce ho sám používáš ve dvou různých smyslech.)
Offline
#7 24. 06. 2010 18:06
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
↑ BrozekP:
bohužel, nějak nechápu co máš na mysli
"Vím, že nic nevím." Sokrates
Offline
#8 24. 06. 2010 18:28
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
1) Tvé q není to q ze zadání. Ty používáš q jako koeficient u absolutního členu v kvadratickém trojčlenu při jednotkovém koeficientu u kvadratického členu. V zadání ale není u  jednička.
jednička.
Pak tam máš dál dokonce jednou  a o chvíli později
a o chvíli později  . Takhle se to nedá psát, musíš to od sebe nějak odlišit.
. Takhle se to nedá psát, musíš to od sebe nějak odlišit.
3a)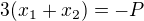
Za 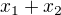 dosadíš
dosadíš  a dostaneš
a dostaneš  (ty tam máš mínus). Pak navíc do
(ty tam máš mínus). Pak navíc do  dosadíš úplně jiné P.
dosadíš úplně jiné P.
Offline
#9 24. 06. 2010 18:38
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
↑ BrozekP:
ok děkuji, musim si na to příště dát větší pozor při přepisování
"Vím, že nic nevím." Sokrates
Offline
#10 24. 06. 2010 21:34
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
Díky moc, strašně jste mi pomohli..mne bylo jasný, že všechno je to pomocí Vietových vztahů, ale nevěděl jsem, jak je použít. Tu 3a jsem nakonec zjistil jak vypočítat, ale nechápal jsem, proč mi stejným postupem nevychází i 3b..Pak jsem zjistil že je potřeba uvést kvadratickou rovnici do základního tvaru, jinak to nejde. Ta 3a totiž vyšla, i když jsem počítal rovnou s 5x^2...Ale ještě jedna věc mi není jasná..pořád nechápu to rozložení a^2 + b^2, resp. to 2. cvičení..hned ten první krok, tu úpravu..nemohl by mi to někdo podrobně popsat? Nebo to je nějaký vzorec? Něco ve stylu (a + b)^2 = a^2 + 2ab + b^2?? Nebo co? Já to fakt nepobírám..
Offline
#11 24. 06. 2010 21:45
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
↑ atomic:
Budu upravovat výraz 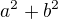 :
:
Při odvozování jsem nejdříve přičetl nulu (to ničemu nevadí), tu jsem si napsal jako  (to je jistě nula) a pak už jen upravoval a použil vzorec
(to je jistě nula) a pak už jen upravoval a použil vzorec 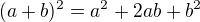 . Platí tedy rovnost
. Platí tedy rovnost .
.
(To si můžeš snadno ověřit roznásobením pravé strany.)
Offline
#13 24. 06. 2010 21:55
Re: Vztahy mezi kořeny a koeficienty kvadratické rovnice
WOW :-O ..to je panečku fígl, to by mne teda nenapadlo ani za nic! ..i když si teď matně vzpomínám, že jsme ho ve škole kdysi dááávno v jedný písemce používali..no každopádně pro mne novota, ale už to nikdy nezapomenu, jak jsem se s tim tady dlouho lámal..každopádně díky moc :)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vztahy mezi kořeny a koeficienty kvadratické rovnice (TOTO TÉMA JE VYŘEŠENÉ)
 na druhou stranu
na druhou stranu