Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 06. 2010 19:13
- <h1>dydy</h1>
- Příspěvky: 161
- Reputace: 0
Stejnoměrná spojitost vs Lipschicovskost
Ahoj, chtěl bych nějak vidět funkci, které je s.s. ale není lip. Z definice sice hezky je vidět, jaké musí být ( u ss musí funkce ležet v obdélníčku, ale nesmí vylézt z horní či dolní strany; u Lip. se udělá ten samý obdélníček, ale funkce nesmí vylézt z úhlopříček). Tedy snad to znáte. No a teď když si oba objekty představíte: obdélník s úhlopíčkou (bod x střed). Je sice vidět že se jedná o různé podmínky, ale nenapadla mě žádná funkce. která by byla ss ale ne lip. Napadne vás nějaká?
Zde je objekt
|-----|
|\ /|
| x |
|/ \ |
|-----|
Opravdu mě nic nenapadlo.
Offline
#2 29. 06. 2010 19:26
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Stejnoměrná spojitost vs Lipschicovskost
Myslím, že 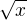 na
na  je stejnoměrně spojitá, ale není lipschitzovská.
je stejnoměrně spojitá, ale není lipschitzovská.
Offline
#3 29. 06. 2010 20:05 — Editoval <h1>dydy</h1> (29. 06. 2010 20:11)
- <h1>dydy</h1>
- Příspěvky: 161
- Reputace: 0
Re: Stejnoměrná spojitost vs Lipschicovskost
No právě. Ale nějaká funkce na R (nebo aspon uprostřed intervalu?
Ale mimochodem (  )' je k
)' je k 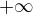 u nuly
u nuly
a nevíte o nějakém pěkné aplikaci, která třeba zobrazí řešení dif rovnic. Wolfram je skvělý, ale například http://www.wolframalpha.com/input/?i=y'=sin(y)ln(x)/x nezobrazí uplně všechny řešení ( 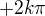 )
)
Offline
#4 29. 06. 2010 20:35
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Stejnoměrná spojitost vs Lipschicovskost
Tak ![kopírovat do textarea $\sqrt[3]x$](/mathtex/13/13f418da1ef0360b934aa90b09d7dd14.gif) . Čemu vadí, že je derivace v nule nekonečná?
. Čemu vadí, že je derivace v nule nekonečná?
Offline
#5 29. 06. 2010 21:02
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Stejnoměrná spojitost vs Lipschicovskost
Tak třeba e^x... není lipschitovská...
Offline
#6 29. 06. 2010 21:04 — Editoval <h1>dydy</h1> (29. 06. 2010 21:26)
- <h1>dydy</h1>
- Příspěvky: 161
- Reputace: 0
Re: Stejnoměrná spojitost vs Lipschicovskost
1:
Ale e^x není zase stejnoměrně spojitá...
Společným znakem stej.spoj a Lip je ,že 1. derivace je omezená (myšleno pro různá x z def oboru,... tzn, že y'(x)<K pro všechny x z def oboru).
Někde jsem našel zmínku, existují i Lip funkce, které derivaci třeba nemají. Škoda že nevím kde a podrbnosti.
A ještě nevíte, kde bych našel nějaká přehled "divných funkcí" ( dirichlet, cantor, čertovy schody, weistrass....)
2:
derivace v nule je nekonečná... Nemůže být tedy Lip, Protože Konstanta Lip by musela být nekoněčně velká (úhlopříčky by tedy šly skoro k sobě)
Offline
#7 29. 06. 2010 21:30
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Stejnoměrná spojitost vs Lipschicovskost
↑ <h1>dydy</h1>:
Nesouhlasím, nemůže to být společným znakem, protože to není znakem stejnoměrné spojitosti. Např. ta třetí odmocnina nemá omezenou první derivaci, přesto je stejnoměrně spojitá.
Edit: K 2: Netvrdím, že třetí odmocnina je lipschitzovská. Tvrdím, že je stejnoměrně spojitá. Na takovou funkci ses ptal.
Offline
#8 30. 06. 2010 09:19 — Editoval Rumburak (30. 06. 2010 09:40)
Re: Stejnoměrná spojitost vs Lipschicovskost
↑ <h1>dydy</h1>:
O funkcích definovaných na intervalu připojím několik poznámek - snad pomohou.
1. Funkce f(x) = |x| je Lipschitzovská , v bodě 0 nemá derivaci.
Avšak každá funkce lipschitzovská je zároveň též absolutně spojitá a tedy s konečnou variací na každém uzavřeném intervalu, tudíž vyjádřitelná
jako rozdíl dvou monotónních funkcí. Má proto vlastní derivaci skoro všude (= až na body množiny o Lebesgueově míře 0).
2. Absolutně spojitá funkce je též stejnoměrně spojitá.
3. Na kompaktním (=uzavřeném) intervalu je stejnoměrně spojitou funkcí KAŽDÁ spojitá funkce, tedy i taková, která nemá derivaci v žádném bodě -
takové spojité funkce existují a dle bodu 1 nemohou být lipschitzovské.
Offline
#9 30. 06. 2010 10:14
Re: Stejnoměrná spojitost vs Lipschicovskost
↑ BrozekP:
Ja myslím, že nie je. Môžeš mi to prosím rozpísať?
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#10 30. 06. 2010 10:33
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Stejnoměrná spojitost vs Lipschicovskost
↑ lukaszh:
Jak napsal Rumburak: „Na kompaktním (=uzavřeném) intervalu je stejnoměrně spojitou funkcí KAŽDÁ spojitá funkce…“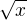 je na
je na ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) spojitá, tedy i stejnoměrně spojitá. Tím, že se omezím na
spojitá, tedy i stejnoměrně spojitá. Tím, že se omezím na  (to bylo zbytečné, měl jsem tam tu jedničku nechat), nic nepokazím. Ale můžu to zkusit dokázat i z definice, pokud budeš chtít.
(to bylo zbytečné, měl jsem tam tu jedničku nechat), nic nepokazím. Ale můžu to zkusit dokázat i z definice, pokud budeš chtít.
Offline
#11 30. 06. 2010 10:52
Re: Stejnoměrná spojitost vs Lipschicovskost
↑ BrozekP:
Ja mám problém hlavne s tou nulou. Dokázať to bez nuly viem. Skôr by som to pochopil dôkazom z definície. Vďaka.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#12 30. 06. 2010 11:27 — Editoval Rumburak (30. 06. 2010 16:56)
Re: Stejnoměrná spojitost vs Lipschicovskost
↑ lukaszh:
K důkazu věty "Funkce spojitá na intervalu [a, b] je na tomto intervalu stejnoměrně spojitá" je potřeba využít kompaktnosti intervalu [a, b] ,
snad nejlépe přes Borelovu větu.
Momentálně jsem v časové tísni, doplním případně později.
Offline
#13 30. 06. 2010 11:39
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Stejnoměrná spojitost vs Lipschicovskost
Dokazuji tedy![kopírovat do textarea $\forall \varepsilon>0\,\exists\delta>0\,\forall x,y\in[0,1]:\quad|x-y|<\delta\Rightarrow|\sqrt x-\sqrt y|<\varepsilon$](/mathtex/45/453b9c6de16f44b261bb0a1565740737.gif) .
.
Pro libovolné  zvolím
zvolím 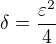 . Dále mějme libovolné
. Dále mějme libovolné ![kopírovat do textarea $x,y\in[0,1]$](/mathtex/73/73977a3396025cd91558bdcf359d01b1.gif) , bez újmy na obecnosti
, bez újmy na obecnosti  (případ
(případ  je triviální a
je triviální a  bychom vyřešili analogicky k následujícímu postupu). Mohou nastat následující varianty:
bychom vyřešili analogicky k následujícímu postupu). Mohou nastat následující varianty:
1) 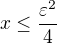 :
:
Protože předpokládáme  , musí být
, musí být  .
.
2)  :
:
Podle Lagrangeovy věty o střední hodnotě existuje 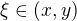 takové, že
takové, že
Offline
#14 30. 06. 2010 13:20
Re: Stejnoměrná spojitost vs Lipschicovskost
↑ BrozekP:
Ďakujem. Už je mi to jasné. Môj problém spočíval v tom, že som nevedel odhadnúť výraz
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#15 30. 06. 2010 17:00 — Editoval Rumburak (07. 07. 2010 15:29)
Re: Stejnoměrná spojitost vs Lipschicovskost
Doplňuji slíbený obecný důkaz.
Mějme funkci f spojitou na intervalu ![kopírovat do textarea $I = [a, b]$](/mathtex/2b/2b66363ed921b5546ff70409c102ef59.gif) a zvolme
a zvolme  . K bodu
. K bodu ![kopírovat do textarea $x \in [a,b]$](/mathtex/80/8016ba03824df7a164abac843589cc05.gif) nechť je
nechť je  takové, že
takové, že (značíme
(značíme  ).
).
Takže
(0) jsou-li 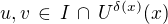 , potom
, potom  .
.
Označme  ,
, 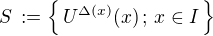 .
.
Množina S je zřejmě otevřeným pokrytím intervalu I (tj. každý bod intervalu I leží v některé množině systému S) a podle Borelovy věty
existuje konečná  , která je rovněž (tedy "stále ještě") pokrytím intervalu I. Existují proto body
, která je rovněž (tedy "stále ještě") pokrytím intervalu I. Existují proto body
(1) 
intervalu I takové, že 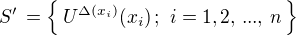 . Položme
. Položme 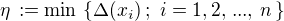 .
.
Zvolme 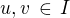 tak, aby
tak, aby  .
. 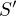 je pokrytí intervalu I, proto mezi body (1) existuje
je pokrytí intervalu I, proto mezi body (1) existuje  takový, že
takový, že 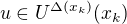 .
.
Ze vztahů 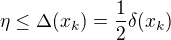 plyne
plyne
1) 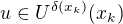
2)  , tedy rovněž
, tedy rovněž 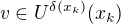 .
.
Z (0) pak dostáváme  .
.
K danému číslu  jsme tak našli
jsme tak našli  takové, že
takové, že  .
.
Není těžké přepsat důkaz do tvaru s abstraktními metrikami (pokud definiční obor funkce f je kompaktní).
Offline
