Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Snadná řada z IMC (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 08. 2010 00:47
Snadná řada z IMC
Vzhledem k tomu, že podobné úlohy se zde již několikrát řešily, neměl by tento činit vážnější potíže.
Určete součet řady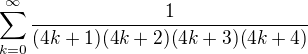 .
.
Offline
- (téma jako vyřešené označil(a) Olin)
#2 07. 08. 2010 14:57 — Editoval Marian (07. 08. 2010 15:00)
Re: Snadná řada z IMC
↑ Olin:
Existuje jistě mnoho metod, jak spočítat tuto nekonečnou řadu. Po několika pokusech, které se mi příliš nelíbily, jsem našel celkem elegantní způsob, jak celou věc zajistit. Budu potřebovat pouze základní poznatky o potenčních řadách, především ten, který hovoří o stejnoměrné konvergenci.
Offline
#3 15. 08. 2010 21:04
Re: Snadná řada z IMC
↑ Marian:
Řešení je samozřejmě správně. Mimochodem, ve vzorovém řešení je uvedena i varianta pomocí čtyřnásobné integrace. Danou úlohu lze řešit však i bez jakéhokoliv integrování, pokud
Offline
#4 16. 08. 2010 08:31
Re: Snadná řada z IMC
↑ Olin: Jistě, čtyřnásobná integrace mě napadla hned. Ale zrovna toto považuji za krajně nechutné řešení. Proto jsem uvedl řešení s jedinou itnegrací (snad to bude poučné pro zájemce o tuto problematiku). Tím je navíc vyřešena úloha kompletně. Přerovnávání známých řad mě napadlo také, ale museli bychom (jak píšeš) předpokládat znalost součtu. A tomu jsem se vědomě vyhýbal.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Snadná řada z IMC (TOTO TÉMA JE VYŘEŠENÉ)


 pro
pro ![kopírovat do textarea $x\in (0,1]$](/mathtex/9e/9e8f8a22fc0e728a953b2ad52e121465.gif) takto:
takto:
 dostaneme tudíž
dostaneme tudíž
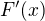 zapsat jako lineární kombinace čtyř geometrických řad, které budou konvergentní. Proto
zapsat jako lineární kombinace čtyř geometrických řad, které budou konvergentní. Proto



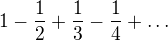 a
a 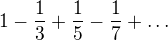 .
.