Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 04. 2008 14:19
- Honza Bohuslav
- Zelenáč
- Příspěvky: 19
- Reputace: 0
Přijímací zkouška z matematiky
Na břehu řeky stojí strom a na něm sedí ve výšce 12 m pták. Na protějším břehu ve vzdálenosti 20 m stojí druhý strom a na něm sedí pták ve výšce 10 m. Oba vyletí současně a stejnou rychlostí za rybou, která pluje těsně pod hladinou a oba k ní doletí současně. Jak daleko od břehů pluje ryba?
Offline
#2 03. 04. 2008 15:59
Re: Přijímací zkouška z matematiky
↑ Honza Bohuslav:
Ryba pluje od břehu 8,9 m nebo od druhého ptáka na druhé straně 11,1 m.
Offline
#6 03. 04. 2008 19:08 — Editoval Ginco (03. 04. 2008 19:10)
Re: Přijímací zkouška z matematiky
↑ ttopi: tak já to rozepíši: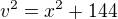
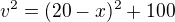
-----------------------------------------------------------------------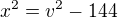
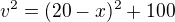
---------------------------------------------------------------------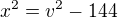

-------------------------------------------------------------------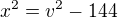
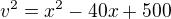
--------------------------------------------------------------------
dosadim levou stranu 1. rovnice místo x^2 do 2. rovnice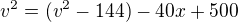
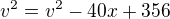

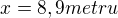
Tu výšku jsem nepočítal, poněvadž jsem šel hned po x .
Je to už srozumitelné?
edit: Jo, už vím,proč to bylo nesrozumitelné: místo v jsem ve 3. řádku použil a. ( vše opraveno)
Offline
#8 03. 04. 2008 19:14 — Editoval Ginco (03. 04. 2008 19:18)
Re: Přijímací zkouška z matematiky
↑ ttopi:
Jo jasně tvůj postup je dobrý, ale bohužel nechci tvrdit, že je i pro mě přirozenější, protože pokud počítám podobné úlohy, tak používám právě to, že si část rozdělím na  a druhou na
a druhou na 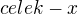
Ale v jednom se shodnem : vyšlo to stejně :)
Offline
#9 03. 04. 2008 19:17 — Editoval ttopi (03. 04. 2008 19:17)
Re: Přijímací zkouška z matematiky
Já přece taky. Pak tam mam c+d=20, takže dosadím za c=20-d. Jenom to tam nechci hned motat a chci aby to bylo nejdřív jen s tím c a d pro jednoduchost a při lámání chleba dosadím co je třeba. To je stylem už :-)
Spíš cest je více, řešení je stejné :-)
oo^0 = 1
Offline



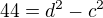
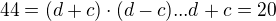
 ..
.. 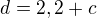 ->
->  a z toho
a z toho 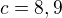
 a pak mi to přijde zmatené .. Já nevim :-)
a pak mi to přijde zmatené .. Já nevim :-)