Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 04. 2008 14:23
- Honza Bohuslav
- Zelenáč
- Příspěvky: 19
- Reputace: 0
Povrch krychle
Povrchy obou krychlí, z nichž jedna má hranu o 22 cm delší než druhá, se od sebe liší o 19272 cm2 (čtverečních). Vypočítejte délku hran obou krychlí.
Offline
#3 03. 04. 2008 17:05
- Honza Bohuslav
- Zelenáč
- Příspěvky: 19
- Reputace: 0
Re: Povrch krychle
Jenomže když ty neznámé přehodím na druhou stranu tak se mi obě vyloučí a pak by to vyšlo, že úloha nemá řešení,což se mi nezdá
Offline
#6 03. 04. 2008 17:39
- Honza Bohuslav
- Zelenáč
- Příspěvky: 19
- Reputace: 0
Re: Povrch krychle
a jak to teda mám upravit aby mi vypadlo to x2
Offline
#8 03. 04. 2008 17:49
- Honza Bohuslav
- Zelenáč
- Příspěvky: 19
- Reputace: 0
Re: Povrch krychle
ja to ale pořád nechápu, když to y dosadím do té spodní rovnice tak dostanu 6x2+2904=6x2+19272 a zase se mi 6x2 zmizí
Offline

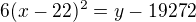
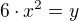
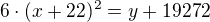
 a zbude
a zbude  , tedy
, tedy 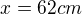
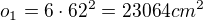


 se nerozloží jako
se nerozloží jako  ale podle vzorce
ale podle vzorce  . Takže tady to
. Takže tady to  . No pak už nevadí že ti vypadne
. No pak už nevadí že ti vypadne  , protože ti tam zůstane
, protože ti tam zůstane 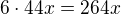 . Chápeš?
. Chápeš?