Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 08. 2010 17:53 — Editoval medvidek (24. 08. 2010 17:58)
Re: Přechodový děj 2. řádu
↑ kotry:
V podstatě vše správně.
Jediná chyba (která se zatím nikam dál nepromítá) je ve výpočtu  . Chybí tam dvojka ve jmenovateli v členu, který máš zakroužkovaný a označený jako beta.
. Chybí tam dvojka ve jmenovateli v členu, který máš zakroužkovaný a označený jako beta.
Další postup:
Konstanty  a
a 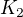 se dopočtou z počátečních podmínek.
se dopočtou z počátečních podmínek.
První podmínka je  . Z vyjádření průběhu proudu v čase
. Z vyjádření průběhu proudu v čase  pak vyplyne vztah
pak vyplyne vztah  .
.
Druhá podmínka by měla být pro derivaci proudu v čase  , máme však podmínku
, máme však podmínku  . Ta je ovšem ekvivalentní, souvislost je dána rovnicí, u které jsi skončil. Na začátku dějě bude tedy platit
. Ta je ovšem ekvivalentní, souvislost je dána rovnicí, u které jsi skončil. Na začátku dějě bude tedy platit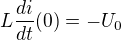 .
.
Průbeh derivace proudu už máš také vyjádřen. Po dosazení z počáteční podmínky pro derivaci proudu vyplyne vztah .
.
Máme tedy dva vztahy pro dvě neznámé  a
a 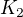 ...
...
EDIT: Zbývá ještě řešit případ podkritického (a kritického útlumu), kdy char. rovnice nemá dva reálné kořeny.
Offline
#5 24. 08. 2010 22:04
Re: Přechodový děj 2. řádu
↑ medvidek:
tam nemá být nula, když ten proud v 0 je 0 ?? když tam dám -U/L tak mi nevyjde K1=-K2
Offline
#6 24. 08. 2010 22:23
Re: Přechodový děj 2. řádu
↑ kotry:
Jedna rovnice je pro proud: (1)
(1)
a druhá rovnice je pro derivaci proudu: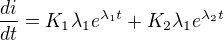 (2)
(2)
Pro  je
je  , to říkáš správně, proto jsme dostali z PRVNÍ rovnice vztah
, to říkáš správně, proto jsme dostali z PRVNÍ rovnice vztah  .
.
Pro  je ve DRUHÉ rovnici
je ve DRUHÉ rovnici 
(ne tedy nula, jak jsi tam napsal na začátku: 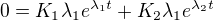 ).
).
Dole na tom samém papíře už ale máš napsáno toto ,
,
což už je správně. To je vlastně rovnice (2) s využitím podmínky  a
a  .
.
Offline
 má být vždy znaménko mínus před
má být vždy znaménko mínus před  .
. , dále to ale máš už dobře (nerovná se to
, dále to ale máš už dobře (nerovná se to  , ale
, ale  ).
).