Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Vyjádření kořenů neřešitelné rovnice za pomocí kořenů jiné rovnice
#1 29. 08. 2010 17:52
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Vyjádření kořenů neřešitelné rovnice za pomocí kořenů jiné rovnice
Označme podmínku P(n) jako:
Kořeny obecné rovnice n-tého stupně nejsou vyjádřitelné pomocí "elementárních" operací (+,-,*,/, odmocnina) mezi koeficienty této rovnice.
Např. platí P(5).
Otázka: existuje obecná rovnice n-tého stupně taková, že platí P(n) a že kořeny této rovnice jsou vyjádřitelné pomocí "elementárních" operací (+,-,*,/, odmocnina) mezi koeficienty této rovnice a mezi kořeny nějakých rovnic, jejichž stupeň je menší než n?
(Tj. rovnice R sama není řešitelná, avšak pokud můžeme použít ve vyjádření jejich kořenů kořeny jiné neřešitelné rovnice (nebo rovnic) s nižším stupněm, pak již za jejich pomoci rovnice R řešitelná je. Je to taková "relativizovaná" řešitelnost.)
"Máte úhel beta." "No to nemám."
Offline
#2 29. 08. 2010 18:07
Re: Vyjádření kořenů neřešitelné rovnice za pomocí kořenů jiné rovnice
no pokud mám polynom stupně n>=5 a znám n-1 jeho kořenů (tj. kořeny nějakého polynomu stupně n-1), pak i pátý kořen snandno dopočítám. ale možná jsi to myslel nějak jinak
Offline
#3 29. 08. 2010 18:45
Re: Vyjádření kořenů neřešitelné rovnice za pomocí kořenů jiné rovnice
Vezmu "neřešitelnou" rovnici 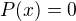 (P je polynom stupně alespoň 5) a vytvořím z ní rovnici
(P je polynom stupně alespoň 5) a vytvořím z ní rovnici 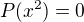 . Tato je taky "neřešitelná" (jinak bychom pomocí ní snadno vyřešili původní rovnici) a má vyšší stupeň než původní, avšak její kořeny zase snadno vyjádříme pomocí kořenů původní rovnice.
. Tato je taky "neřešitelná" (jinak bychom pomocí ní snadno vyřešili původní rovnici) a má vyšší stupeň než původní, avšak její kořeny zase snadno vyjádříme pomocí kořenů původní rovnice.
Offline
#4 29. 08. 2010 20:34
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Vyjádření kořenů neřešitelné rovnice za pomocí kořenů jiné rovnice
↑ Olin:
To je pravda, ale 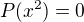 není obecná ve smyslu "libovolných" koeficientů u mocnin
není obecná ve smyslu "libovolných" koeficientů u mocnin 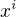 (neřekl jsem, pravda, co mám na mysli pod pojmem "obecná rovnice").
(neřekl jsem, pravda, co mám na mysli pod pojmem "obecná rovnice").
Pod pojmem "obecná rovnice n-tého stupně" mám na mysli rovnici  pro obecné hodnoty
pro obecné hodnoty  ,
, 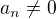 . A úkolem je vyjádřit kořeny této rovnice dle výše uvedených pravidel. Rovnice
. A úkolem je vyjádřit kořeny této rovnice dle výše uvedených pravidel. Rovnice 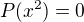 je jistý speciální případ nějaké obecné rovnice, není však obecná.
je jistý speciální případ nějaké obecné rovnice, není však obecná.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Vyjádření kořenů neřešitelné rovnice za pomocí kořenů jiné rovnice
