Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 09. 2010 14:23
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Obsahují přirozená čísla nekonečno?
Doteď jsem tak nějak žil v představě, že nekonečno je součástí přirozených čísel.
Ale našel jsem definici, podle které je množina konečná, jestliže její mohutnost náleží do přirozemých čísel. Takže to nekonečno mi tam teď nesedí. A vlastně si také vzpomínám, že jsme kdysi v analýze pracovali s množinou reálných čísel obsahují nekonečno, značili jsme ji R*.
Takže je pravda, že nekonečno není součástí přirozených (a tedy ani celých, racionálních a reálných) čísel?
Offline
- (téma jako nevyřešené označil(a) jelena)
#3 02. 09. 2010 14:32
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Obsahují přirozená čísla nekonečno?
↑ Stýv:
Jasně, díky za potvrzení. Teď mě napadá spousta věcí, které by v přirozených číslech s nekonečnem vlastně nefungovaly (vč. sčítání), jen mě to dřív nenapadlo.
Offline
#4 02. 09. 2010 14:46 — Editoval Rumburak (02. 09. 2010 14:52)
Re: Obsahují přirozená čísla nekonečno?
↑ teolog:
Naproti tomu když budujeme reálná čísla pomocí Dedekindovy metody řezů v množině rac. čísel (viz V. Jarník: Diferenciální počet I)
a odhlédneme-li od podmínky, že každá z množin A,B tvořících řez (A/B) je neprázdná, pak lze položit 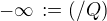 ,
, 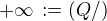 ,
,
kde Q je množina všech racionálních čísel. Považovat  za reálná čísla proto není tak nepřirozené, jak by se snad mohlo zdát.
za reálná čísla proto není tak nepřirozené, jak by se snad mohlo zdát.
Přirozenými ani celými či racionálními čísly však  nejsou.
nejsou.
Offline
#5 02. 09. 2010 14:56
Re: Obsahují přirozená čísla nekonečno?
↑ Rumburak: nj, ale pak by se to muselo ošetřit při definici sčítání apod.
Offline
#7 02. 09. 2010 19:36
Re: Obsahují přirozená čísla nekonečno?
Pracujeme-li s rozšířeným množinovým universem, můžeme získat přirozená čísla, která obsahují i nekonečné přirozené číslo (větší než všechna standardní). Bohužel mám k tomuto tématu jen velmi stručné materiály a příliš se v nich neorientuji, takže nejsem schopen poskytnou moc dalších informací.
Offline
#8 03. 09. 2010 08:49 — Editoval Rumburak (03. 09. 2010 09:40)
Re: Obsahují přirozená čísla nekonečno?
↑ Olin:
Já myslím, že to je věc definice. Pokud se rozhodneme přirozenými čísly nazývat právě všechna konečná ordinální čísla, jak se v teorii množin
(alespoň v ZF, GB) děje, tak žádné rozšíření množinového universa na tom nic nezmění - nebo jde o něco, čemu už vůbec nerozumím.
Offline
#9 03. 09. 2010 13:29
Re: Obsahují přirozená čísla nekonečno?
Velmi stručný úvod do této problematiky je tady, ale přiznávám, že tomu nerozumím prakticky vůbec. 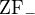 značí běžnou ZF teorii bez axiomu fundovanosti.
značí běžnou ZF teorii bez axiomu fundovanosti.
Offline
#11 08. 09. 2010 11:16
Re: Obsahují přirozená čísla nekonečno?
Zdravím opět po delší době.
Přirozená čísla jsou samozřejmě jen konečná. Rozšíření univerza je samozřejmě možné, ale to na definici nic nemění.
Jen ještě doplním zajímavost. Pokud bychom uvažovali množinu přirozených čísel s jedním nestandardním prvkem (nekonečnem), tak takováto množina může být modelem Robinsonovy aritmetiky. Peanovu aritmetiku už na to ale bohužel nenapasujem:-)
↑ Olin: Ten odkaz je z čeho? ze Sochora?
Dva jsou tisíckrát jeden.
Offline
#12 08. 09. 2010 12:49
Re: Obsahují přirozená čísla nekonečno?
↑ Wotton:
To jsem naskenoval materiály, které nám na "přednášce" rozdával doc. Mlček. Ještě od něj mám zavedení reálných čísel pomocí rozšíření a končí to myslím řešením diferenciálních rovnic pomocí rozšíření :-) Předtím nám rozdal své základy teorie množin od axiomů po kardinální aritmetiku, stacionární množiny a delta-rozklady. Vše je to na nemnoha papírech A4 (nesmírně husté), v případě zájmu mohu naskenovat (bohužel nám to nechtěl dát v elektronické podobě).
Offline