Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Campbell-Baker-Hausdorffova formule – speciální případ
#1 10. 01. 2010 22:17 — Editoval BrozekP (05. 09. 2010 23:25)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Campbell-Baker-Hausdorffova formule – speciální případ
Tuto úlohu nám zadal cvičící z kvantové mechaniky. Termín odevzdání je dnešek, ale i kdyby se tu řešení do půlnoci objevilo, tak ho nebudu vydávat za své, slibuji :-). Protože úlohu považuji za zajímavou a myslím, že pro některé členy fóra může být výzvou, tak jsem ji zařadil do zajímavých úloh.
Hranaté závorky jsou komutátory, tj. např. ![kopírovat do textarea $[A,B]=AB-BA$](/mathtex/76/765bed93426637063d0d1d7f53d737a5.gif) . A, B a C jsou čtvercové matice takové, aby vše mělo dobrý smysl (sám moc nevím, co všechno bych po nich měl požadovat, možná už ani není nutné nic dodávat). Exponenciela matice je definována řadou, tedy
. A, B a C jsou čtvercové matice takové, aby vše mělo dobrý smysl (sám moc nevím, co všechno bych po nich měl požadovat, možná už ani není nutné nic dodávat). Exponenciela matice je definována řadou, tedy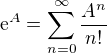
Zadání:
Nechť
a
. Ukažte, že
a nalezněte, co patří místo otazníčku.
Offline
#2 06. 09. 2010 14:04
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Campbell-Baker-Hausdorffova formule – speciální případ
Offline
#4 07. 09. 2010 11:52
Re: Campbell-Baker-Hausdorffova formule – speciální případ
↑ jarrro:
Jak bys chtěl nad konečným tělesem definovat exponenciálu matice?
Offline
#6 07. 09. 2010 12:35 — Editoval Olin (07. 09. 2010 12:38)
Re: Campbell-Baker-Hausdorffova formule – speciální případ
↑ jarrro:
Tím pádem bude v konečném tělese (alespoň v 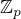 ) od nějakého
) od nějakého  dál platit
dál platit  , což nemá multiplikativní invers, který v exponenciále potřebuješ.
, což nemá multiplikativní invers, který v exponenciále potřebuješ.
Řečeno zajímavěji: Má-li těleso nenulovou charakteristiku, pak je její faktoriál v tomto tělese roven nule.
Offline
#8 07. 09. 2010 12:49
Re: Campbell-Baker-Hausdorffova formule – speciální případ
↑ jarrro:
Stále mám pochybnosti. Kolik bude v tělese racionálních čísel 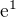 ?
?
Offline
#9 07. 09. 2010 18:20 — Editoval jarrro (07. 09. 2010 18:21)
Re: Campbell-Baker-Hausdorffova formule – speciální případ
↑ Olin:1 je číslo nie matica ja vravím o exponenciále matíc teda 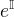 bude v maticiach nad poľom racionálnych čísel to isté ako nad poľom reálnych čísel I je jednotková matica nie jednotka v danom poli,alebo som zas mimo?
bude v maticiach nad poľom racionálnych čísel to isté ako nad poľom reálnych čísel I je jednotková matica nie jednotka v danom poli,alebo som zas mimo?
MATH IS THE BEST!!!
Offline
#10 07. 09. 2010 18:45 — Editoval Olin (07. 09. 2010 18:45)
Re: Campbell-Baker-Hausdorffova formule – speciální případ
Můžeš brát moji jedničku jako matici 1x1 :-) Ale je to jedno, stejně dobře můžeš exponencializovat jednotkovou čtvercovou matici libovolné velikosti. Jinak já měl pocit, že 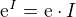 a v tělese racionálních čísel jaksik éčko nenacházím…
a v tělese racionálních čísel jaksik éčko nenacházím…
Jinak navrhuji tuto diskusi přesunout, ať nezaneřáďujeme toto téma věnované jinému problému.
Offline
#12 07. 09. 2010 18:51
Re: Campbell-Baker-Hausdorffova formule – speciální případ
↑ Olin:aha fakt bože ja som idiot dúfam,že predpoklad na to pole,aby bolo okrem charakteristiky nula aj úplné(limita postupnosti jeho prvkov je jeho prvok)už bude stačiť ale ako sa poznám zas nie
MATH IS THE BEST!!!
Offline
#13 07. 09. 2010 22:26
Re: Campbell-Baker-Hausdorffova formule – speciální případ
On asi krapet problém je s tím, že exponenciála je definována pomocí řady, tedy limity, což spíše než algebraické vlastnosti vyžaduje nějaké topologické.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Campbell-Baker-Hausdorffova formule – speciální případ
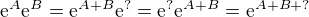
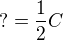
 .
.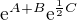 upravit. Víme, že
upravit. Víme, že ![kopírovat do textarea $[A+B,\frac12C]=0$](/mathtex/df/df182e7b696064a6878fab0f5e6f4f8a.gif) a
a ![kopírovat do textarea $[[A+B,\frac12C],A+B]=[0,A+B]=0$](/mathtex/9c/9cb91c519477f13645bd84064f314792.gif) ,
, ![kopírovat do textarea $[[A+B,\frac12C],\frac12C]=[0,\frac12C]=0$](/mathtex/8f/8f37517b6fa2c363bb57e4b99d380011.gif) , můžeme tedy použít rovnost (1) (kde
, můžeme tedy použít rovnost (1) (kde  bude nahrazeno
bude nahrazeno 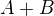 ,
,  bude nahrazeno
bude nahrazeno 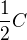 a
a  bude nahrazeno komutátorem
bude nahrazeno komutátorem ![kopírovat do textarea $[A+B,\frac12C]$](/mathtex/36/3630dd1cbb73ab8a6587d1fb03e91f7a.gif) ).
).![kopírovat do textarea $\mathrm{e}^{A+B}\mathrm{e}^{\frac12C}=\mathrm{e}^{A+B+\frac12C}\mathrm{e}^{\frac12[A+B,\frac12C]}=\mathrm{e}^{A+B+\frac12C}\mathrm{e}^{0}=\mathrm{e}^{A+B+\frac12C}$](/mathtex/d1/d148286f24eabd36843a8ea32f34e63d.gif)
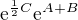 :
:![kopírovat do textarea $\mathrm{e}^{\frac12C}\mathrm{e}^{A+B}=\mathrm{e}^{\frac12C+A+B}\mathrm{e}^{\frac12[\frac12C,A+B]}=\mathrm{e}^{A+B+\frac12C}\mathrm{e}^{0}=\mathrm{e}^{A+B+\frac12C}$](/mathtex/bf/bfb1dbced8bc1b6883ac49e3069d2311.gif)
 ,kde 1 je jednotka v poli)
,kde 1 je jednotka v poli)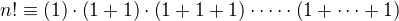 v poslednom činiteli je n sčítancov
v poslednom činiteli je n sčítancov