Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 09. 2010 15:53 — Editoval hradecek (15. 09. 2010 15:55)
Goniometrická rovnica




Mám to správne ?
Ako bude vyzerať konečný výsledok ?
Ako sa mám dostať k takémuto výsledku ? Wolfram
Díky.
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
- (téma jako vyřešené označil(a) hradecek)
#3 16. 09. 2010 06:40 — Editoval Honzc (16. 09. 2010 06:43)
Re: Goniometrická rovnica
↑ hradecek:
Jak už psal↑ Stýv:, tak je potřeba buď důsledně používat zapsání výsledku v obloukové míre (tj.  ), nebo obojí v úhlové
), nebo obojí v úhlové
(tj.  )
)
Protože perioda u tangens je  , tak
, tak  jsou už obsaženy v té periodě.
jsou už obsaženy v té periodě.
Až toto spravíš, tak to budeš mít stejně jako Wolfram, protože  je těch
je těch  a to
a to 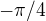 je
je
Offline

 je paskvil. používej buď stupně, nebo radiány. pak to třeba i uvidíš;)
je paskvil. používej buď stupně, nebo radiány. pak to třeba i uvidíš;)