Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » úloha z diskrétní matematiky (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 09. 2010 17:18
úloha z diskrétní matematiky
Dokažte, že (n^4 + 4) není prvočíslo pro každé n z množiny N kromě 1 .. tzn. n>1
Mohl by mi s tím někdo poradit?
---------------------------------------------------------------------
Dopracovala jsem se akorát k takovému "důkazu", že:
použila jsem Wilsonovu větu
předpokládala jsem, že (n^4 + 4) JE prvočíslo a dosadila ho za "p" (a doufala, že přijdu ke sporu)
upravila rovnici
a vyšlo mi
(n^4 + 4)! = -1 , což nelze > SPOR
napadá vás někoho důkaz jiný?
Nic, co jsem použila jsme ještě nebrali, takže ani nevím, zda jsem všechny vzorce použila správně. Dostali jsme tento úkol "dobrovolně".
Děkuji za pomoc
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
- (téma jako vyřešené označil(a) Esperance)
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » úloha z diskrétní matematiky (TOTO TÉMA JE VYŘEŠENÉ)

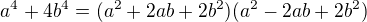 :)
:)