Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 14. 04. 2009 16:58
Re: Kombinatorika
↑ Rumburak:plS brachO pomozte ja mam zajtra pisomku s toho a potrebujem co najrychlejsie rozoznat variacie od kombinacii. dakujem
Offline
#4 14. 04. 2009 18:21 — Editoval ttopi (14. 04. 2009 18:23)
Re: Kombinatorika
↑ kubO:
Je to celkem jednoduché.
Variace - záleží na pořadí - například při frontě na maso, při různých losovacích soutěží, kde musíš uhádnout třeba pětičíslí, nebo když se volí třeba předseda, zástupce, náměstek atd...
Kombinace - nezáleží na pořadí - například tvorba volejbalového mužstva, sportka, atd...
S opakováním/bez opakování - už z názvu lze odvodit, čeho se to týká. S opakováním je třeba tvorba petičíslí z cifer 2;3;5 - je jasné, že se tam, musí nějaká opakovat. Nebo třeba když se tvoří telefonní čísla, nebo značky aut, mohou se tam číslice opakovat.
Jinak doporučuji Wiki a následující odkazy:
Kombinace
Variace
Permutace
oo^0 = 1
Offline
#6 15. 04. 2009 09:19 — Editoval Rumburak (06. 10. 2010 11:14)
Re: Kombinatorika
Přiznám se, že pojetí středoškolské kombinatoriky nepovažuji za příliš šťastné. Tak především: definice variací a kombinací se opírají o pojmy jako
"skupina", "zálaží/nezáleží na pořadí", "prvky se mohou/nemohou opakovat", které do matematiky nepatří a mohou tak vyvolávat rozpaky a nejasnosti,
dále: dvojice pojmů variace - variace s opakováním, kombinace - kombinace s opakováním nevystihují způsobem své konstrukce vztahy mezi
obecným a speciálním, které zde existují - ba právě naopak tyto vztahy zatemňují.
Pokud bych měl do těchto záležitostí co mluvit, postavil bych středoškolskou kombinatoriku poněkud jinak. Rád bych zde tuto alternativu předložil
k případné diskusi. Pojmy, které jsou míněny v "mém" pojetí, píši vždy v uvozovkách, v závěru příspěvku je pak dám do souvislostí se standardní terminologií -
standardní termíny budu psát velkými písmeny.
A. VARIACE (bez ohledu na případné opakování). Nechť jsou dány m-prvková množina M a množina K = {1,2,...,k} , již nazveme "množinou pozic".
I d e a : Určit variaci z prvků množiny M znamená určit funkci (=zobrazení), která každé pozici z množiny K přiřadí některý prvek množiny M.
D e f i n i c e . "Variací k-té třídy (nebo též: délky k) prvků množiny M (nebo též: z m prvků )" nazýváme funkci z množiny K do množiny M
(tj. D(f) = K, H(f) je částí M). Je-li tato funkce prostá, hovoříme o "prosté variaci", případně o "variaci bez opakování".
B. KOMBINACE (bez ohledu na případné opakování). Nechť je opět dána m-prvková množina M.
I d e a : Určit kombinaci prvků z množiny M znamená ke každému prvku množiny M určit počet jeho výskytů v této kombinaci.
D e f i n i c e . "Kombinací prvků množiny M (nebo též: z m prvků )" nazýváme funkci f z množiny M do množiny {0,1,2, ...} . Dále nazýváme
- číslo f(x) "počtem výskytů prvku x v kombinaci f" ,
- číslo 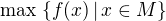 jejím "typem",
jejím "typem",
- číslo  její třídou (nebo též "délkou").
její třídou (nebo též "délkou").
O kombinacích "typu" 1 hovoříme jako o "kombinacích bez opakování".
Souvislosti se standardní terminologií (pojmy uvádím v jednotném čísle):
VARIACE k-TÉ TŘÍDY Z m PRVKŮ = "prostá variace k-té třídy z m prvků",
VARIACE k-TÉ TŘÍDY Z m PRVKŮ S OPAKOVÁNÍM = "variace k-té třídy z m prvků - bez ohledu na to, zda je prostá",
KOMBINACE k-TÉ TŘÍDY Z m PRVKŮ = "kombinace k-té třídy z m prvků, jejíž typ je roven 1",
KOMBINACE k-TÉ TŘÍDY Z m PRVKŮ S OPAKOVÁNÍM = "kombinace k-té třídy z m prvků - jejíž typ může být libovolný".
Offline
#7 06. 10. 2010 12:30
Re: Kombinatorika
↑ Rumburak:
Rozumím důvodům a zčásti s nimi souhlasím.
Na druhou stranu mi navržený přístup nepřijde šťastně navržený. Konstrukce kombinací je zbytečně technická.
Kolik je kombinací 7. třídy z 5 prvků, jejíž typ je roven 3?
Offline
#8 06. 10. 2010 14:18 — Editoval Rumburak (07. 10. 2010 14:17)
Re: Kombinatorika
↑ petrkovar:
Především děkuji za reakci.
Navržená definice kombinací se mi osvědčila ke srozumitelnému odvození vzorce pro počet C'(n,k) klasikých kombinací s opakováním.
Ale netvrdím, že tento systém je bez nedostatků.
K té úloze "Kolik je kombinací 7. třídy z 5 prvků, jejíž typ je roven 3?":
Pokoušet se o odvození obecného vzorce jsem zatím nepovažoval za nutné, ale tuto výzvu výhledově přijímám.
Prozatím jen konkretně a schematicky, určitě to bude srozumitelné i bez podrobného komentáře:
7 = 3 + 1 + 1 + 1 + 1 ...... počet možností : 5 ,
7 = 3 + 2 + 1 + 1 + 0 ...... počet možností : 5*4*3 ,
7 = 3 + 2 + 2 + 0 + 0 ...... počet možností : 5*(4 nad 2) *)
7 = 3 + 3 + 1 + 0 + 0 ...... počet možností : 5*4*3 , OPRAVA: 5*(4 nad 2) obdobně jako o řádek výše
tedy pokud jsem se někde nesekl.
*)... využil jsem toho, že případ "2 + 2 + 0 + 0" má stejný počet možností jako případ "1 + 1 + 0 + 0" .
Jak tuto úlohu zformulovat v klasických pojmech ? Bylo by to komplikovanější a připadá mi, ža ani řešení by nebylo snazší.
Offline
#9 06. 10. 2010 22:13
Re: Kombinatorika
↑ Rumburak:Vztah pro počet kombinací s opakováním se odvozuje "klasicky" s využitím "oddělovačů". Mám za to, že je to snadno vstřebatelné i dobře zapamatovatelné. Samozřejmě závisí na konkrétním podání (jako se vším ;-)
Nerad bych, aby to vyznělo, že je třeba trápit se se vzorcem. (Řekl bych, že nejlépe jej lze odvodit s využitím inkluze a exkluze). Chtěl jsem říci, že uvedená definice se snaží obejít pojem "s opakováním" a místo toho zavádí pojem "typ". Ve zcela analogickém, jen více technicky náročném kontextu.
Uvedená definice variace vychází z pojmu zobrazení, přičemž předpokládá dobré zvládnutí tohoto pojmu. Moje zkušenost se studenty techniky je, že zobrazení je téměř výhradně probíráno na nekonečných spojitých množinách (nerozlišujeme "zobrazení" a "funkce"). Naproti tomu mají informatici dobře zažitý pojem posloupnosti (jednorozměrné pole) a tak variace zavádíme jako posloupnosti, jejíž prvky vybíráme (s opakováním/bez opakování) z nějaké konečné množiny.
Největším kamenem úrazu nejsou definice ani vzorečky (u zkoušky je povolena jedna strana A4 s poznámkami), ale samotné porozumění zadání u slovních úloh. V kombinatorice tato slabina hodně vyčnívá. Srovnejme s diferenciálním počtem, limitami, integály, soustavy rovnic... Tam obvykle vzoreček trčí ze zadání.
Offline
#10 07. 10. 2010 11:20 — Editoval Rumburak (07. 10. 2010 14:06)
Re: Kombinatorika
↑ petrkovar:
Ten "typ" u "kombinace" jsem zavedl jen proto, aby se jeho prostřednictvím zjednodušila definice kombinace bez opakování. Bez tohoto
v podstatě pomocného pojmu by jistě bylo možno se obejít, pokud by se ukázalo, že další uplatnění už nemá.
Zkušenosti učitele respektuji a jsem rád, že jste (jsi) se se mnou o ně podělil. Hledisko učit látku takovým způsobem, aby počet studentů,
kteří ji správně pochopí a dovedou použít, byl co největší, je samozřejmě správné.
Mezi důvody, proč jsem se snažil najít ke SŠ kombinatorice alternativní cestu, hrál svoji významnou a možná i hlavní roli právě onen vzpomínaný
vzorec pro počet kombinací s opakováním, jehož důkaz metodou "oddělovačů", jak byl prezentován v učebnici, jsem tehdy vůbec nepochopil
(což byla v "mé" matematice na SŠ jedna z velmi mála situací tohoto druhu a je možné, že i jediná, protože na další takovou se nepamatuji)
a myslím, že i dnes bych s tím měl problém, o naději takovýmto způsobem vzorec samostatně odvodit ani nemluvě - teprve přes ty funkce jsem
do toho začal vidět.
Možná že jenom nejsem "kombinatorický typ" - i v běžném životě mne leká, musím-li čelit velkému množství možností. :-)
EDIT . Zakončím tento příspěvek úsměvnou příhodou: Jeden můj známý se sklony k lehce sadistickému humoru - učitel statistiky na VŠ -
také studentům povoloval u zkoušky "tahák" - ovšem pouze formátu A5 a tahák musel být "přihlášen". Když jistý student přišel s tahákem
velikosti A4, dotyčný učitel mu jej přetrhl na dvě půlky a dal mu vybrat, kterou půlku si chce ponechat.
Offline
#11 07. 10. 2010 21:31 — Editoval petrkovar (06. 11. 2010 20:41)
Re: Kombinatorika
↑ Rumburak:My povolujeme jednu STRANU A4. S Möbiovým listem zatím nikdo nepřišel...
Offline
