Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 10. 2010 15:33 — Editoval Esperance (09. 10. 2010 15:35)
sumy

mohl by mi někdo vysvětlit PROČ se to takto posunuje? zatím jsem slyšela jen samé "tohle dej sem a to sem".. "proč?".. "prostě se to tak dělá"
díky moc
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#3 09. 10. 2010 15:41
Re: sumy
výhodné vím, že to je. Myslela jsem vysvětlení typu: j dáš do první sumy. J v prvním případě nabývá nejvýše i (a i nabývá nejvýše n) proto je v první sumě j=1 až n.. a pak nějak vysvětlit i tu druhou
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
#4 09. 10. 2010 15:48
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: sumy
Pokud si nakreslíš do roviny dvojice [i,j], přes které se sčítá, jako body, měla bys vidět, že jeden způsob znamená nejprve sčítání po řádcích a pak sečtení sloupců, druhý způsob je sčítání po sloupcích a pak sečtení řádků.
Offline
#6 09. 10. 2010 16:17
Re: sumy
díky, je mi to trochu jasnější.
Náhodou nevíte o stránkách, kde jsou pravidla pro počítání se sumami shrnuty? A nějaké fígle:) (sama bych asi neviděla, že sumu k^2, mám počítat jako rozdíl sum (k+1)^3 - sum k^3 )
hezký den
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
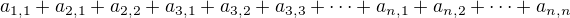 a druhá
a druhá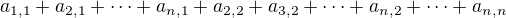 z toho to pekne vidíš,že sa to rovná
z toho to pekne vidíš,že sa to rovná