Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 10. 2010 12:31
Re: Mocniny s neznámou
↑ phill05: Nejprve uprav výraz v závorce a poté umocni na -2. Bude to tak přehlednější. Víš, jak se pracuje s mocninami?
Offline
#3 16. 10. 2010 12:41
Re: Mocniny s neznámou
Ja jsem to vypočítal jenže nevím jestli je to tak správně. Nejprve jsem přehodil zlomek protože je závorka na -. Umocnil jsem závorku vnitřní((2c)4tou) a přemístil neznámou se záporným exponentem na opačné strany, dále si nejsem jistý zda c na 0-tou je c, takže jsem očítal s c. Dále vypočítal mocniny.
Offline
#5 16. 10. 2010 12:51 — Editoval mountdoom (16. 10. 2010 12:57)
Re: Mocniny s neznámou
↑ phill05: jakekoliv 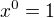 , dokonce i
, dokonce i  . Nemusíš s ním tedy vůbec počítat. To, co jsi provedl by bylo s
. Nemusíš s ním tedy vůbec počítat. To, co jsi provedl by bylo s 
Offline
#9 16. 10. 2010 13:04
#14 16. 10. 2010 13:33
#15 16. 10. 2010 13:39
Re: Mocniny s neznámou
↑ mountdoom:
Děkuji, zeditováno. Máš dobré oči. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#16 16. 10. 2010 13:42
#17 16. 10. 2010 13:58
Re: Mocniny s neznámou
↑ mountdoom:lebo napr. limita  kde
kde nemusí byť jedna,ale sa môže meniť podľa funkcií
nemusí byť jedna,ale sa môže meniť podľa funkcií
MATH IS THE BEST!!!
Offline
#20 16. 10. 2010 15:06
Re: Mocniny s neznámou
↑ mountdoom:tak v niektorých oblastich matematiky je účelné definovať  napr.v kombiantorike alebo v teórii množín v kombinatorike napr. z nula prvkov sa dá jedným spôsobom vybrať 0 prvkov v teórii množín počet zobrazení prázdnej množiny do prázdnej množiny je jedno prázden zobrazenie a podobne
napr.v kombiantorike alebo v teórii množín v kombinatorike napr. z nula prvkov sa dá jedným spôsobom vybrať 0 prvkov v teórii množín počet zobrazení prázdnej množiny do prázdnej množiny je jedno prázden zobrazenie a podobne
v iných oblastiach ako napr. matematická analýza to je naopak neprípustné napr. z dôvodu uvedeného v mojom predchádzajúcom príspevku
MATH IS THE BEST!!!
Offline

 , to se zkrátilo na
, to se zkrátilo na  po umocnění tedy vznikne
po umocnění tedy vznikne  .
.
