Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 10. 2010 18:04
Goniometrické výrazy, rovnice
Zdravím.
Na tohle fórum jsem zavítal dnes poprvé. A jelikož zítra budu psát písemku na výše uvedené téma, tak jsem zde přišel pro pomoc. Nemám totiž kontakt na nikoho kdo by Matiku nějak ovládal, nebo spíše na někoho, kdo by si tohle učivo střední školy pamatoval.
Skoušel jsem se to učit, ale bohůžel se to za jeden den naučit nedá. Pochopil jsem akorát to co jsem se kdysi učil na základce a k tomu Sinovu a Kosinovu větu.
Na tu písemku mám zadání a potřeboval bych k těmhle čtyřem příkladům výpočet a nějaký běžný postup.
http://img140.imageshack.us/img140/6954/matika.png
Jestli to pro mě někdo vypočítá, tak mu předem děkuju..
Offline
- (téma jako vyřešené označil(a) jelena)
#2 18. 10. 2010 18:10 — Editoval b.r.o.z1 (18. 10. 2010 18:36)
Re: Goniometrické výrazy, rovnice
Příklad 1
Kdy je zlomek definován? pokud jeho jmenovatel se nerovná nule přeci(dělit nulou neumíme)
Zjednodušení, mrkni do tabulek na vzorce:  ,
,  ,
,  3 vzorečky, které stačí znát na zjednodušení ;-)
3 vzorečky, které stačí znát na zjednodušení ;-)
po zjednodušení ti vznikne tg x...ten je taky definovaný jen za určitých podmínek ;-)
Příklad 2
opět vzorečky jako u 1
Příklad 3
vědět že:  - to nepoužiješ, ale dobré vědět, za to použiješ:
- to nepoužiješ, ale dobré vědět, za to použiješ: 
cotg taky není při nějakém úhlu definován.... to je Df
zjednodušíš pomocí  a vzorců z 1
a vzorců z 1
Příklad 4
opět vzorec  nahradíš
nahradíš 
Pak substituce za 
dopočítáš "a" a dostadíš zpět do substituce => máš hodnoty x
"Vím, že nic nevím." Sokrates
Offline
#9 18. 10. 2010 19:00 — Editoval b.r.o.z1 (18. 10. 2010 19:00)
Re: Goniometrické výrazy, rovnice
↑ gadgetka::-) to říkáš jako kdyby ti bylo vela:-):-) mladá dračice:-D
udělej 2., jdu na to 3:-)
"Vím, že nic nevím." Sokrates
Offline
#17 19. 10. 2010 21:06 — Editoval strakosh (20. 10. 2010 08:24)
Re: Goniometrické výrazy, rovnice
Ahoj, potřeboval bych prosím poradit s úpravou výrazu :
http://forum.matweb.cz/viewtopic.php?id=21555
Offline
#18 19. 10. 2010 21:10 — Editoval gladiator01 (20. 10. 2010 09:06)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: Goniometrické výrazy, rovnice
EDIT
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#19 30. 10. 2010 21:29 — Editoval hudecekl (30. 10. 2010 22:33)
Re: Goniometrické výrazy, rovnice
Hezký večer, mám velkou prosbu :-) Potřeboval bych pro bratra od přítelkyně vypočítat goniometrické výrazy. Pošlu je email. Prosím o pomoc. Děkuji Lukáš
Příklady jsem uložil na uložto.cz - mam je jen ve formatu jpeg :-(
http://www.ulozto.cz/6387796/73965-1402 … 6944-n-jpg
Offline
#20 30. 10. 2010 21:34
- VojtechSejkora
- Příspěvky: 176
- Reputace: 5
Re: Goniometrické výrazy, rovnice
↑ hudecekl:
a proč je nedáš sem?:-o
Offline
#21 30. 10. 2010 21:50 — Editoval gladiator01 (31. 10. 2010 11:27)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: Goniometrické výrazy, rovnice
↑ strakosh:↑ hudecekl:
Oba dva založte vlastní téma a sem dejte upozornění s odkazem. Za chvíly by se v tom nedalo vyznat.
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#22 28. 02. 2011 15:04 — Editoval djsipic (28. 02. 2011 15:04)
Re: Goniometrické výrazy, rovnice
↑ b.r.o.z1:

muzu se zeptat, jak se došlo k tomuhle? :P děkuju :)
Offline
#23 28. 02. 2011 15:10
- Dana1
- Host
Re: Goniometrické výrazy, rovnice
↑ djsipic:
sin je záporný v 3. a 4. kvadrante, kde sa uhly zapisujú : pí + alfa (3. kvadrant) a 2pí - alfa (4. kvadrant), kde alfa je uhol z 1. kvadrantu (medzi 0 a pí/2), ku ktorému patrí sinus rovný 1/2



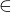 Z}
Z}



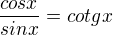

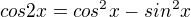
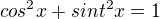


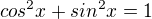 =>
=> 






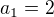

 ... sin takové hodnoty nedostahuje, obor hodnot je od <-1,1> takže 2 tam nepatří
... sin takové hodnoty nedostahuje, obor hodnot je od <-1,1> takže 2 tam nepatří