Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vzorce na derivaci funkci (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 10. 2010 17:39 — Editoval Joerex (24. 10. 2010 17:39)
Vzorce na derivaci funkci
Zdravim,potreboval bych nekde sehnat vzorce na derivaci funkce s absolutni hodnotou,exponencialni a logaritmicke funkce.Ve spouste prikladu jsem se prave kvuli temto funkcim zasekl a byla to pro me konecna.Zkousel jsem googlit,ale bez vysledku.
Diky.
Offline
- (téma jako vyřešené označil(a) Joerex)
#2 24. 10. 2010 17:47
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Vzorce na derivaci funkci
↑ Joerex:
Tak základní vzorce jsou téměř kdekoliv, např. i na wikipedii.
A pokud jde o derivaci funkce s absolutní hodnotou, tak tam bych postupoval jako u řešení rovnic s abs. hodnotou. Tedy bych si funkci rozdělil podle nulových bodů a řešil derivaci na každém intervalu zvlášť. Ukázkový příklad jsem nalezl po zadání do google derivace absolutní hodnota hned na první nabídnuté stránce.
Mimo téma: docela by mne zajímalo, jak probíhalo Vaše hledání.
Offline
#3 24. 10. 2010 18:04
Re: Vzorce na derivaci funkci
Tak abych uvedl treba priklad.
mel jsem derivaci exp. funkce e^((1/x)+1) a z toho vzniklo ((1/x)'+1')*e^((1/x)+1) ,ale podle ceho se to delalo jsem nenasel
pripadne zde je abs.hodnota (|x+1|)' -> (1'+1)*|x+1| to cele lomeno x+1 ...zde jsem take nevedel jak se k tomu dopracovalo
na math.feld jsem se koukal,na wikinu take...takze bud neumim hledat nebo jsem to prehledl
Offline
#4 24. 10. 2010 18:17 — Editoval teolog (24. 10. 2010 18:19)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Vzorce na derivaci funkci
↑ Joerex:
Aha, tak v tom případě zřejmě není problém, jak derivovat exponenciální funkci, ale jak derivovat funkci složenou. I na to existuje pravidlo, které ve stručnosti říká, že derivace složené funkce je rovna derivaci vnitřní krát derivace vnější.
Ve Vašem příkladu 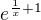 je vnější funkce
je vnější funkce  , kde
, kde  a vnitřní je funkce
a vnitřní je funkce 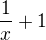 .
.
Takže podle pravidel pro derivaci exponenciální funkce a funkce složené je: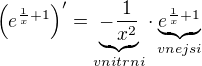
Offline
#5 24. 10. 2010 18:25 — Editoval teolog (24. 10. 2010 18:26)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Vzorce na derivaci funkci
A ještě tedy postup pro tu absolutní hodnotu: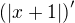
pro x>-1 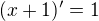
pro x<-1 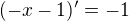
A jak vypadá derivace pro x=-1? V tomto bodě derivace neexistuje, pouze jednostranné derivace (zleva i zprava). Graf má v tomto bodě "špičku".
Offline
#6 24. 10. 2010 18:50 — Editoval Joerex (24. 10. 2010 18:53)
Re: Vzorce na derivaci funkci
Takže pokud mám k dispozici tyhle vzorce http://math.feld.cvut.cz/sedlacko/vzs.pdf tak bych s tim měl vlastně dát dokupy všechny derivace. V tom případě jsem pouze nedokázal funkci zakomponovat do vzorce.
Offline
#8 24. 10. 2010 19:26
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: Vzorce na derivaci funkci
↑ teolog:
anebo: (|x+1|)'=(x+1)/|x+1|
Offline
#9 24. 10. 2010 19:28
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Vzorce na derivaci funkci
↑ maly_kaja_hajnejch-Lazov:
Díky, já jsem si říkal, že by to šlo vyjádřit i nějak jednotně, ale tohle mne nenapadlo.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vzorce na derivaci funkci (TOTO TÉMA JE VYŘEŠENÉ)