Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 25. 10. 2010 21:54
Re: hody kostku
Offline
#5 25. 10. 2010 22:01
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: hody kostku
↑ myrek:
Pane Mirku,
od minula jste se nějak nepoučil. Pokud po nás něco chcete, tak se od vás očekává nějaká slušnost. Náznak řešení po vás už raději ani chtít nebudu, stačí mi zatím slušnost.
Děkuji.
Offline
#6 25. 10. 2010 22:21
Re: hody kostku
↑ petrkovar:
ano to sice nemůžeme vědět
ale uvedu příklad hodím kostkou a padne mi pět různých čísel (např 1,2,3,4,1,5)
pak udělám další pokus a padnou tři různá čísla (např. 1,2,1,3,3,1)
no a kdybych to takhle udělal dejme tomu milionkrát tak dostávám reprezentativní vzorek, a vím že třeba nejčastěji padnou čtyři různá čísla.
na to bych potřeboval nějakej vzorec?
Offline
#7 25. 10. 2010 22:26
Re: hody kostku
↑ halogan:
ted nejak nevim o cem mluvite pokud vim tak sem o tomto problemu neinformoval mailem ani jinak jak jste minule zadal at vam neposilam maily tak pokud vim vam je skutecne neposilam
z cehoz plyne ze sem se odminule poucil
pokud tento problem nechcete ci neumite resit tak se k nemu nevyjadrujte
naopak bych mohl rict ze vase komentare jsou neslusne
Offline
#8 25. 10. 2010 22:28
Re: hody kostku
↑ myrek:Aha!
Je třeba určit pravděpodobnost každé přípustné možnosti jedno různé číslo, dvě různá čísla, tři čísla, ... n čísel.
Potom se tyto pravděpodonosti dosadí do vztahu pro střední hodnotu náhodné veličiny udávající počet různých čísel při n hodech.
Jak vypadá pravděpodobnost pro jediné číslo při n hodech? Jak pro dvě čísla?
Offline
#9 25. 10. 2010 22:31
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: hody kostku
↑ myrek:
Já bych váš problém možná i dokázal vyřešit (pokud bych chápal zadání). Tady záleží na jedné věci: pokud víme, jak se daná kostka chová (není nijak upravená), tak platí vše jak má (nemusí se nic zkoušet) a dá se s tím normálně počítat. Pokud jde o nějak upravenou kostku, tak na to můžete jít třeba přes frekvenci a sledovat limitu takových experimentů. Na to je potřeba ale víc informací.
K té slušnosti: Mně teď nejde už o maily. Stále to je ale daleko od ideálu. Taky přijdete k doktorovi se slovy "Bolí mě xyz, spravte mě!" — věřím, že ne. Pozdravíte a slušně ho požádáte o radu. To po vás chci i tady, nic víc, nic míň. My tu pracujeme dobrovolně, nemáme z toho materiálně nic, jen takový ten hezký hřejivý pocit, že jsme někomu pro nás neznámému pomohli.
Offline
#10 25. 10. 2010 22:40
Re: hody kostku
↑ petrkovar:
pravdepodobnost toho ze padne 6x po sobe nejake jedno a to same cislo by mela byt 
Offline
#11 25. 10. 2010 23:04
Re: hody kostku
↑ halogan:
kostka není nijak upravena muzete ji povazovat za dokonaou hraci kostku
jak rikam v jednom pokusu hodite sestkrat kostkou a padne vam pět různých čísel (např 1,2,3,4,1,5)
pak uděláre další pokus a padnou vam tři různá čísla (např. 1,2,1,3,3,1)
atd.
Offline
#15 26. 10. 2010 08:53
Re: hody kostku
Ano na 6 hodu ji hodit nemusite (ale muzete ji hodit i napoprve jak jsem psal takova interpretace je ale chybna!) ale kdyz milionkrat hodite kostkou tak byste mel zjistit ze je tam sestka zastoupena priblizne v jedne sestine hodu, tyto úlohy jsou skutečně takto zadány jde jen o to přijít na jejich správnou interpretaci.
takze jak rikam odpoved na otazku kolikrát musím hodit abych hodil sestku je sestkrat! je to zrejme nejaky prumer ci stredni hodnota (?)
ale vratme se k teto uloze ktera je zadana podobne a zrejme by mela mit i podobnou interpretaci tedy zrejme nejaka prumerna hodnota
Offline
#16 26. 10. 2010 09:38
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: hody kostku
Kostka ma sest ruznych hodnot a muze padnout vzfy prave jedna. Kostka neni nijak upravena, takze ma kazda hodnota stejnou pravdepodobnost padnuti. Jelikoz pravdepodobnost sjednoceni musi byt 1 (alespon jedna hodnota musi padnout, neboli kostka nemuze spadnout na hranu), tak pravdrpodobnost padnuti kazde hodnoty je 1/6.
V realu to znamena, ze kdyz hodite milionkrat, kazdou hodnotu hodite nejspis zhruba 1000000/6x. To s temi sesti hody neni uplne spravne.
Nejsem ted u pocitace, takze to pisi trochu strucne a vynechavam nektere casti teorie, jestli bude zajem, tak odpoledne to doplnim presneji.
Offline
#18 26. 10. 2010 13:35
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: hody kostku
↑ myrek:
Dobře, tak tohle řeknu malému dítěti. A ono se zeptá "A co když hodím pokaždé pětku?" :-)
Prostě nemůžete říct, že do šesti hodů šestku aspoň jednou hodim. Ani kdybyste hodil kostkou milionkrát, tak nemáte jistotu, že hodíte šestku.
Co mohu spočítat, je třeba "Kolikrát musím hodit kostkou, abych měl alespoň 90% šanci, že mi padne aspoň jedna šestka?" To není složité. Ale je to něco jiného, než žádáte.
Pravděpodobnost není o jistotě (teda kromě jistých a nemožných jevů :-), je to o šanci, nebo chcete-li průměrné hodnotě při velkém počtu opakování jistého experimentu.
Offline
#19 26. 10. 2010 14:10 — Editoval pietro (26. 10. 2010 14:11)
Re: hody kostku
Ahoj , tu som hodil 1000x 6 kociek. Súčet čísel je 21013.
..next?
Offline
#21 26. 10. 2010 14:20
Re: hody kostku
↑ halogan:Neviem, nečítal som ju celú, len som reagoval na prvé "zadanie" a možno sa sformuluje čo chcel autor povedať.
Offline
#22 26. 10. 2010 14:23
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: hody kostku
↑ pietro:
Potíž je v tom, že jeden náhodně vygenerovaný sample nám toho moc neurčí. Vám můžu vygenerovat 6 tisíc hozených šestek, to je též stejně pravděpodobné. Výsledek je třeba spočítat, ne jen si hrát s generátory.
A poprosil bych příště, abyste si diskuse četl. Už jsme se od původního dotazu dostali někam jinam.
Děkuji.
Offline
#23 26. 10. 2010 14:27
Re: hody kostku
↑ halogan:Áno ospravedlňujem sa Ti, už druhýkrát som vstúpil ( čiste iba v zápale boja) do Tvojej konverzácie s niekym iným.
Offline
#24 26. 10. 2010 21:02
Re: hody kostku
↑ halogan:
ano je pravda ze nemam jistotu
ale vratme se radeji zpet k puvodni uloze!
konzultoval sem to a dostal sem za odpoved tento navod k reseni
pravdepodobnost toho ze nam padne jedno a to same cislo nekolikrat po sobe je:

pravdepodobnost ze padne vsech n cisel z mnoziny 1 až n je:

a já potřebuuji zjistit  což je pravděpodobnost že dostanu k různých čísel
což je pravděpodobnost že dostanu k různých čísel
a mám zřejmě najít pro jaké k bude ta pravděpodobnost největší.
Offline
#25 26. 10. 2010 22:19
Re: hody kostku
↑ myrek:Abychom vyjádřili hodnotu 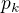 , zkusíme ji nejprve popsat. Číslo
, zkusíme ji nejprve popsat. Číslo 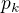 udává pravděpodobnost, že v
udává pravděpodobnost, že v  hodech padne PRÁVĚ
hodech padne PRÁVĚ  růzbých hodnot. K tomu použijeme princip inkluze a exkluze.
růzbých hodnot. K tomu použijeme princip inkluze a exkluze.
Snad jsem neudělal chybu, nějak se mi ten vztah nelíbí.
Ještě doplním: nehledáme takové 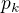 , které je největší, ale střední hodnotu náhodné proměnné udávající počet stejných číslic při n hodech.
, které je největší, ale střední hodnotu náhodné proměnné udávající počet stejných číslic při n hodech.
Například střední hodnota počtu puntíků při jednom hodu kostkou je  .
.
Offline