Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 14. 04. 2008 15:07
Re: problem s n! faktorialom
↑ faktorial:vyňal som ten "menší" faktoriál pred zátvorku a vykrátil napr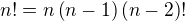
MATH IS THE BEST!!!
Offline
#9 14. 04. 2008 18:51 — Editoval jarrro (14. 04. 2008 18:56)
Re: problem s n! faktorialom
↑ faktorial:vôbec nie ty v tom máš ale riadny chaos počúvaj najprv si uvedom ktoré číslo je väčšie a ako idú prirodzené čísla zaradom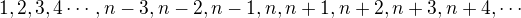 potom je ešte potrebné pozna? rekurentnú definíciu faktoriálu
potom je ešte potrebné pozna? rekurentnú definíciu faktoriálu 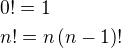
MATH IS THE BEST!!!
Offline


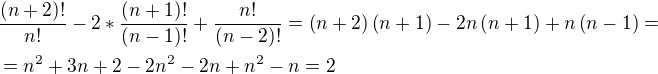
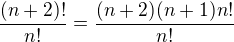
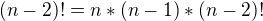
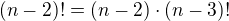
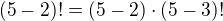
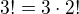
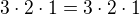



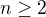
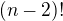 .
.