Matematické Fórum

dal jsem ty vektory do zápisu matice ale mate mě tam ta nula na diagonále, v jakém případě se dají vyměňovat řádky?

0  1  2 l 0
1 -1  0 l 0
1  0 -2 l 0

vyšlo mi x3 = -4, x2 = -8, x1 = -8 ; teď jen jestli to je dobře

↑ michall:
Co ta čísla znamenají? V zadání se ptají na něco jiného, totiž jestli je ten soubor vektor LN/LZ.

Ale chápu, že to mají být řešení té soustavy rovnic. Ty bys určitě řekl, že jsou to "řešení matice", protože, jak je vidět nechápeš, že ona matice pouze reprezentuje soustavu lineárních algebraických rovnic (jinak by ses neptal na to zaměňování řádků). Kdybys vektory nenaskládal do řádků, ale do sloupců, tak by v tom bylo líp vidět proč jsi sestavil zrovna takovou soustavu - protože by to krásně korespondovalo s definicí lineární nezávoslosti. Takhle řešíme jinou soustavu, takže to tak dobře vidět není - a opíráme se přitom o větu, že řešitelnost obou soustav je stejná (tedy buď mají nenulové řešení obě, nebo ani jedna).
Dál tě nemusí mást nuly na diagonále, žádné tam totiž nejsou. Diagonála je u čtvercové matice "úhlopříčka", ne ten poslední sloupec. Jestli jsem tě teda dobře pochopil.

A to řešení bohužel dobře není. Když si uvědomíš jak vypadá ta zmíněná soustava, budeš si moci udělat zkoušku a přijít na to sám. Musel jsi udělat někde chybu v úpravách. Když je sem pošleš, tak ji najdeme.

↑ michall:
Je to soustava rovnic, že ano? Tak poslední rovnice nám říká, že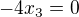

Tak jak to bude s hodnotou x_3?

↑ michall:
Ta SOUSTAVA rovnic má jen triviální řešení, to ano. Ale pokud chceme odpovědět na to, na co se nás v zadání ptají, tak je potřeba z toho udělat nějaký závěr, tedy rozhodnout, jestli ty vektory tvoří LN nebo LZ soubor. Za tím účelem doporučuji podívat se na definici lineární nezávislosti.

Taky si přečti ten můj první příspěvek, kde mj. píšu, že je to lépe vidět v případě, že vektory nenaskládáš do řádků, ale do sloupců matice soustavy. Jakmile uvidíš souvislost té definice a té sestavené soustavy, neměl by být problém z toho vyvodit, jestli to, že soustava má jen triviální řešení implikuje lineární nezávislost nebo závislost.

Edit: koukni se sem, tam se nedávno řešil stejný problém.

↑ michall:
Ano, to jsem taky nahoře napsal, že to tak musí dopadnout. Teď ještě popřemýšlej jak souvisí ta soustava (s vektory ve sloupcích) s tou definicí, kolem které se to celé točí. Pomoct by mohlo to vlákno, na které odkazuju na konci svého minulého příspěvku.