Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 10. 2010 13:57
- gabrielka75
- Příspěvky: 98
- Reputace: 0
permutace
můžeme mi prosím někdo napsat podrobný postup řešení? já tomu vůbec nerozumim moc děkuju
Kolik různých dvojciferných a trojciferných čísel můžeme napsat z číslic 1,2,3,5,7,9tak, aby se číslice neopakovaly?
Offline
- (téma jako vyřešené označil(a) jelena)
#2 29. 10. 2010 14:07
Re: permutace
Mnozina cisel, ktere muzes pouzit....M = (1,2,3,5,7,9)...tzn. 6 cisel
a) dvojciferne moznosti, aby se cislice neopakovaly.... dvojciferne = dve pozice, tzn. na prvni pozici 6 moznost cisel (1,2,3,5,7,9) a na druhou pozici 6-1 (tech 6 cisel minus cislo, ktere pouzijes na prvni pozici), cili celkovy pocet = 6 * (6-1) = 30 moznost
b) 6 * (6-1) * (6-2) = 120 moznosti
-proc (6-2)? protoze jsi si vycerpala 2 moznosti)
Offline
#3 29. 10. 2010 14:19
- gabrielka75
- Příspěvky: 98
- Reputace: 0
Re: permutace
moc děkuji, ale i tak tomu moc nerozumim
Offline
#4 31. 10. 2010 23:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: permutace
↑ gabrielka75:
Zdravím,
buď můžeš postupovat logicky, jak doporučuje kolega ↑ metamedik: (tedy postupným výběrem 1. čísla ze všech a 2. čísla ze všech bez toho, co již bylo vybráno, podobně pro trojciferná čísla).
Nebo použitím vzorců - variace (variace po 2 z 6 prvků pro výběr dvouciferných, variace po 3 z 6 prvků pro výběr trojciferných).
užitečný materiál.
Lze označit za vyřešené? Děkuji.
Offline
#5 01. 11. 2010 08:04 — Editoval gadgetka (01. 11. 2010 08:05)
Re: permutace
a) dvojciferných 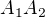
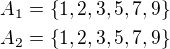
Množina 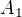 má
má  prvků, množina
prvků, množina 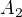 má
má  prvků. Na začátku dvojciferného čísla je jedno číslo z množiny
prvků. Na začátku dvojciferného čísla je jedno číslo z množiny 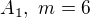 . Číslo z množiny
. Číslo z množiny 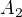 už můžeme vybrat jen z
už můžeme vybrat jen z 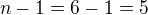 možností, protože to jedno číslo je už použito na pozici prvního čísla. Počet čísel=
možností, protože to jedno číslo je už použito na pozici prvního čísla. Počet čísel=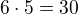
b) trojciferných 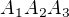
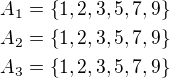
Na prvním místě trojciferného čísla je jedna číslice z množiny 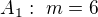
Na druhém místě je jedna číslice z množiny 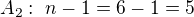
Na třetím místě je jedna číslice z množiny 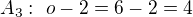
Pokud už je jedna číslice na prvním místě v zápisu čísla, nemůže být na druhém místě, stejně tak, je-li jedna číslice na první pozici a druhá číslice na druhé pozici v zápisu čísla, už nemůžou být použity na třetím místě v zápisu čísla.
Celkem: 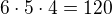
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#6 01. 11. 2010 08:31
- gabrielka75
- Příspěvky: 98
- Reputace: 0
Re: permutace
Gadgetko moc děkuji za vysvětlení
moc si toho vážím
Offline
