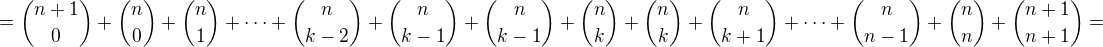Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 03. 11. 2010 08:53 — Editoval apollo1 (03. 11. 2010 08:55)
Re: Důkaz matematickou indukcí
to ečko by se dalo také dokázat takto: vychazí z bynomické věty... stačí vzít (1+1)na n tou ... a když to rozložíš podle vzorce tak ti zbydou jen ty kombinační čísla od n nad nultou až n nad n tou a to se rovná 2 na ntou pac 1+1 na n tou je 2 na ntou (avsak to samozřejmě NENÍ matematická indukce)
Offline
#6 03. 11. 2010 10:35 — Editoval Marian (03. 11. 2010 10:43)
Re: Důkaz matematickou indukcí
↑ apollo1:↑ djsipic: Dokažme tedy indukcí binomickou větu, tj. vztah
Nebudu v dalším diskutovat speciálně o výjimkách 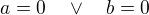 , které se dají ošetřit bez použití této poučky. Vysvětluji to proto, že po aplikaci binomické věty vznikají do jisté míry neurčité výrazy ve tvaru
, které se dají ošetřit bez použití této poučky. Vysvětluji to proto, že po aplikaci binomické věty vznikají do jisté míry neurčité výrazy ve tvaru ![kopírovat do textarea $[0^0]$](/mathtex/1b/1b3f334b52ae4d5932bdf5c19cfe0819.gif) . Připomínám, že definice binomického koeficientu je tato:
. Připomínám, že definice binomického koeficientu je tato:
s přihlédnutím k samozřejmé identitě 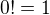 .
.
Tvrzení je platné pro 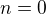 , neboť
, neboť  a zároveň
a zároveň
Předpokládejme nyní (indukční předpoklad), že tvrzení platí i pro nějaké fixní 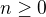 , tedy ekvivalentně
, tedy ekvivalentně
Z toho odvodím, že binomická věta platí i pro  takto:
takto:
Tím je důkaz indukcí kompletní.
Zpět k původní úloze. Dosadíme-li  do binomické věty, řeší to jistě úlohu (e). Pokud bys trval na důkazu cvičení (e) přímo indukcí, stačí v předvedeném důkazu položit všude
do binomické věty, řeší to jistě úlohu (e). Pokud bys trval na důkazu cvičení (e) přímo indukcí, stačí v předvedeném důkazu položit všude 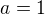 a
a  .
.
Offline
#8 03. 11. 2010 12:37
Offline
#9 03. 11. 2010 14:12
Re: Důkaz matematickou indukcí
↑ zdenek1: Tohle mi nepřipomíná důkaz matematickou induckí.
↑ petrkovar: Nenapadá mě, jak bychom mohli postupovat rychleji metodou matematické indukce. Rád se poučím. Mohu poprosit o náznak řešení.
Offline
#10 03. 11. 2010 14:35
Re: Důkaz matematickou indukcí
↑ Marian:Ten "náznak" je právě v příspěvku ↑ zdenek1:. Je to část inkukčního kroku. Nápověda: co je na levé straně a co na pravé straně v příspěvku autora zdenek1?
Celou úpravu je možno udržet v zápisu pomocí symbolu sumy (s jedním drobným trikem, který je z příspěvku patrný) a pak je uvedená úprava na 1 řádek.
Offline


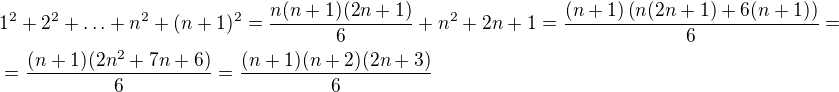 ..dokázáno
..dokázáno