Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#8 03. 11. 2010 22:44
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: podprostor (souřadnice vektoru)
↑ michall: Zpětné dosazení akorát potvrzuje, že x1,x2,x3,x4 jsou hledané souřadnice.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#9 03. 11. 2010 23:10
Re: podprostor (souřadnice vektoru)
Kondr napsal(a):
↑ michall: Zpětné dosazení akorát potvrzuje, že x1,x2,x3,x4 jsou hledané souřadnice.
takže to je vlastně to co jsem potřeboval najít, teď jen to samé pro q(x)...a pokud by tam nebyla ta rovnost?
Offline
#11 04. 11. 2010 23:18
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: podprostor (souřadnice vektoru)
↑ michall:Pokud by rovnost nebyla, někde jsme udělali chybu. Pokud by soustava měla nekonečně mnoho řešení, tak zadané generátory netvoří bázi, protože jsou lineárně závislé. Kdyby soustava neměla žádné řešení, tak zadané generátory opět netvoří bázi 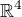 , neboť negenerují celý prostor (a protože jsou čtyři, musí pak být i lineárně závislé).
, neboť negenerují celý prostor (a protože jsou čtyři, musí pak být i lineárně závislé).
Pokud jde o to, proč jsme řešili soustavu rovnic, doporučuju si připomenout definici pojmu "souřadnice" a také fakt, že rovnost mezi vektory znamená rovnost mezi složkami.
Stačí tak?
BRKOS - matematický korespondenční seminář pro střední školy
Offline