Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Equivalence tvrzeni s limitama (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 11. 2010 22:59 — Editoval Keo (03. 11. 2010 23:34)
Equivalence tvrzeni s limitama
Ahoj, mam zadano:
edited: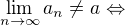 existuje takove okoli Ha bodu a, ze nekonecne mnoho clenu
existuje takove okoli Ha bodu a, ze nekonecne mnoho clenu  v nem nelezi.
v nem nelezi.
Ukolem je prepsat tudle ekvivalenci a dokazat ji.
Kdyz jiteda prepisu tak: <- tato cast je mi je vcelku jasna.. a dal: existuje takove okoli Ha bodu a -
<- tato cast je mi je vcelku jasna.. a dal: existuje takove okoli Ha bodu a - 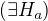 ; a dalsi cast : ze nekonecne mnoho clenu
; a dalsi cast : ze nekonecne mnoho clenu  v nem nelezi. Tak "v nem nelezi" bude opet
v nem nelezi. Tak "v nem nelezi" bude opet  .
.
Otazka ale je, jak zapsat ze nekonecne mnoho clenu a_n? Pujde to primo tak jak je na zacatku? 
Offline
- (téma jako vyřešené označil(a) Keo)
#2 03. 11. 2010 23:28
Re: Equivalence tvrzeni s limitama
Snad je to pokročilou hodinou večerní, ale jsem z tohohle zcela zmaten.
Za prvé si myslím, že uvedená ekvivalence neplatí. Zvolme například  pro každé n. Pak
pro každé n. Pak 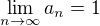 , ale neexistuje žádné okolí jedničky, aby v jeho doplňku leželo nekonečně mnoho členů posloupnosti
, ale neexistuje žádné okolí jedničky, aby v jeho doplňku leželo nekonečně mnoho členů posloupnosti 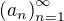 .
.
Za druhé, jak přesně jsi tu ekvivalenci přepsal? Vypadá to, že jsi limitu na levé straně přepsal na negaci její definice. Máš pravdu, že  , ale pokud tedy chceš ekvivalenci přepsat do tvaru
, ale pokud tedy chceš ekvivalenci přepsat do tvaru  , pak bys měl negovat i to B.
, pak bys měl negovat i to B.
"Existuje nekonečně mnoho členů, že" můžeš vyjádřit tak, že existuje vybraná podposloupnost, že všechny její členy mají požadovanou vlastnost. Takže něco jako  .
.
Můžeš prosím nějak dovysvětlit svůj příspěvek? Mám pocit, že mi uniká něco zásadního, ale vůbec nemůžu přijít na to co.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#4 03. 11. 2010 23:36 — Editoval Oxyd (03. 11. 2010 23:36)
Re: Equivalence tvrzeni s limitama
↑ Keo:
A já si teď prozměnu uvědomil, že moje vyjádření nekonečně mnoha členů s danou vlastností je vlastně ekvivalentní vyjádření  . Takže ano, šlo by to tak.
. Takže ano, šlo by to tak.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Equivalence tvrzeni s limitama (TOTO TÉMA JE VYŘEŠENÉ)