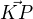Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 15. 04. 2008 22:04
Re: Analytická geometrie
Navod: chce to najit rovnici primky, ktera je kolma na stranu 'b' a prochazi bodem B. Takze nejdriv najdeme smernici 'k' te kolme primky. K tomu nam staci smernice 's' te primky obsahujici stranu 'b'. Pro tyto smernice plati vztah k = -1/s. Jakmile mame 'k', mame vyhrano. Rovnize bude mit tvar y=kx+q. Cislo 'q' dopocteme snadno, nebot vime, ze primka musi prochazet bodem B.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#3 15. 04. 2008 22:06 — Editoval Ginco (15. 04. 2008 22:27)
Re: Analytická geometrie
↑ leniczcha:
Obecná rovnice přímky obsahující v_b, to je to samé jako obecná rovnice výšky v_b
Víme, že výška v_b je spuště na z bodu B[4;2] a má stejný vektor, jako má přímka AC normálový vektor( kolmý na směrový)
tedy směrový vektor AC : 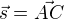
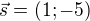 to je směrový vektor přímky procházející body A a C
to je směrový vektor přímky procházející body A a C to je normálový vektor přímky A a C
to je normálový vektor přímky A a C
obecná rovnice výšky tedy bude :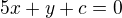
dosadím za x,y souřadnice bodu B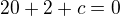
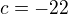
Obecná rovnice výšky v_b tedy bude : 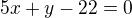
Offline
#4 15. 04. 2008 22:10
Re: Analytická geometrie
↑ Lishaak:
pokud vím, tak obecná rovnice přímky je : nikoliv
nikoliv  toto je směrnicový tvar přímky ne?
toto je směrnicový tvar přímky ne?
Offline
#7 15. 04. 2008 22:21 — Editoval jelena (15. 04. 2008 22:23)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analytická geometrie
↑ Ginco:
Drobna poznamka: smernicovy vektor AC je zaroven normalovym vektorem vysky - tedy neni nutne nejak upravovat, ale rovnou pouzit do obecne rovnice vysky. Souhlasis?
Editace: drobna poznamka uz byla udelena, tak ta moje je zbytecna - rusim :-)
Offline
#8 15. 04. 2008 22:22 — Editoval Jorica (15. 04. 2008 22:30)
Re: Analytická geometrie
Z texem si nerozumim, zkusim to po tobe opravit, to bych mohla zvladnout ;-)
směrový vektor AC : 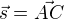 to je směrový vektor přímky a soucasne to je normálový vektor hledane vysky v_b
to je směrový vektor přímky a soucasne to je normálový vektor hledane vysky v_b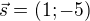
obecná rovnice výšky tedy bude :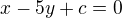
dosadím za x,y souřadnice bodu B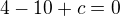
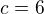
Obecná rovnice výšky v_b tedy bude : 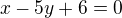
Offline
#11 22. 04. 2008 21:05
Re: Analytická geometrie
Nevím si rady s tím, jak vyjádřit z obecné rovnice přímky parametrický tvar. Vím, že je to lehké, ale neznám ten správný vzorec.
Příklad: Přímka p je dána obecnou rovnicí 2x + 5y - 6 = 0. Vyjádřete přímku p parametrickými rovnicemi. Poradíte někdo, prosím?
Díky
Offline
#12 22. 04. 2008 21:16
Re: Analytická geometrie
V prvom rade si vyjadris normalovy vektor : n = (2,5). Z neho ziskas smerovy: s = (5,-2).
Teraz potrebujes este suradnice jedneho bodu priamky, napr pre y=0 bude bod A[x;0] s x=3. Ked poznas smerovy vektor a bod, je to uz lahke.
x=3+5t
y=-2t kde t patri R
7902 5 01 gymnázium - matematika - Okt.... holt maturity
-------------------------------------------------------------------
Bejvávalo. Momentálne FMV B-ME-MO prez [sem. 5, E] a s tym spojena matematika a statistika ma sem opat priviala.
Offline
#14 22. 04. 2008 21:26
Re: Analytická geometrie
Bavime sa o tej istej priamke? Lebo [0,2] jej nepatri...
7902 5 01 gymnázium - matematika - Okt.... holt maturity
-------------------------------------------------------------------
Bejvávalo. Momentálne FMV B-ME-MO prez [sem. 5, E] a s tym spojena matematika a statistika ma sem opat priviala.
Offline
#19 23. 04. 2008 19:18
#20 23. 04. 2008 20:37
Re: Analytická geometrie
jedno z moznych reseni, doufam ze spravne ;)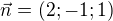 normalovy vektor roviny je smerovy vektor primky na rovinu kolme, napiseme tedy parametricke vyjadreni primky kolme na rovinu a obsahujici bod A
normalovy vektor roviny je smerovy vektor primky na rovinu kolme, napiseme tedy parametricke vyjadreni primky kolme na rovinu a obsahujici bod A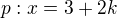
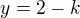
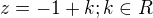
najdeme prusecik teto primky a roviny dosazenim do obecne rovnice roviny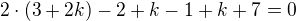
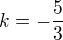
prusecik ziskame dosazenim do parametricke rce primky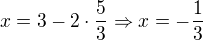
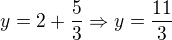
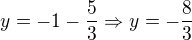
![kopírovat do textarea $P=[-\frac13;\frac{11}{3};-\frac{8}{3}]$](/mathtex/f9/f97d7492dce1c67f3388ce17e523a030.gif)
ted muzeme vypocitat vzdalenost bodu P a A, coz je i vzdalenost bodu A od roviny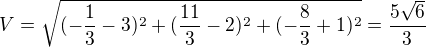
bod A' ziskame posunutim bodu P o vektor 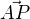
![kopírovat do textarea $P+(P-A)=[-\frac13;\frac{11}{3};-\frac{8}{3}]+[-\frac{10}{3};\frac53;-\frac53]=[-\frac{11}{3};\frac{16}{3};-\frac{13}{3}]$](/mathtex/c8/c880260ffe53a7e6f0c01c5f780701aa.gif)
![kopírovat do textarea $A'=[-\frac{11}{3};\frac{16}{3};-\frac{13}{3}]$](/mathtex/ec/ec3a39c42197febd8c11cacc2bdc0e28.gif)
Offline

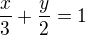
![kopírovat do textarea $Px=[3;0];Py=[0;2]$](/mathtex/f2/f265c0a725fd3674bd60bbc8c5e0d7d8.gif)
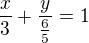
![kopírovat do textarea $M=[m;0]$](/mathtex/e9/e98151b7a616f7705bd87f17ac6b857f.gif) (y=o pak lezi na ose x)
(y=o pak lezi na ose x)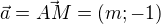
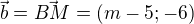
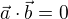
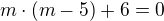
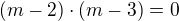
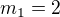

![kopírovat do textarea $M=[2;0]$](/mathtex/a9/a9fecc5ba08d7f123c53327f3c8078fc.gif) a
a ![kopírovat do textarea $M=[3;0]$](/mathtex/1c/1c156d947961617646594f66bbff82e5.gif)

![kopírovat do textarea $S_{bc}=[\frac12;-1];S_{ab}=[-1;\frac32]$](/mathtex/bf/bf4120db9dd7471c41f625cca81a49d8.gif)
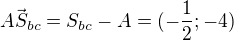
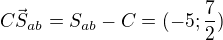
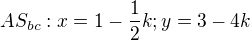
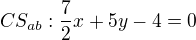
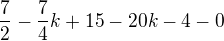

![kopírovat do textarea $P=[1-\frac{58}{174};3-\frac{4\cdot58}{87}]=[\frac23;\frac13]$](/mathtex/b5/b5e33161f36ffbffa62794b4507ede05.gif)
![kopírovat do textarea $A'=T+\vec{AT}=[\frac23;\frac13]+[-\frac13;-\frac83]=[\frac13;-\frac73]$](/mathtex/4b/4be27cf73b72095ce5969245f26ea1f8.gif)
![kopírovat do textarea $B'=T+\vec{BT}=[\frac23;\frac13]+[\frac{11}{3};\frac13]=[\frac{13}{3};\frac23]$](/mathtex/88/881f48fa0e696fad67883d9a930ab4fa.gif)
![kopírovat do textarea $C'=T+\vec{CT}=[\frac23;\frac13]+[-\frac{10}{3};\frac73]=[-\frac83;\frac83]$](/mathtex/a9/a921ce256ce2102dabfd8863c19b4f49.gif)