Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 11. 2010 00:42
A zase ty logaritmy
Offline
- (téma jako nevyřešené označil(a) jelena)
#2 04. 11. 2010 06:17
Re: A zase ty logaritmy
↑ matanic:
1) Máš dobře zadání?
2)



Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 04. 11. 2010 06:22
Offline
#4 04. 11. 2010 06:30
Re: A zase ty logaritmy
↑ matanic:
 obě strany zlogaritmovat
obě strany zlogaritmovat





Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#8 04. 11. 2010 07:16 — Editoval Cheop (04. 11. 2010 07:19)
#10 04. 11. 2010 07:23
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: A zase ty logaritmy
↑ gadgetka:
Krátila jsi celou rovnici výrazem log x
a jak víš, tak když krátíš musíš to zahrnout do výsledku.
Nikdo není dokonalý
Offline
#12 04. 11. 2010 08:02
Re: A zase ty logaritmy
Cheop napsal(a):
↑ gadgetka:
Krátila jsi celou rovnici výrazem log x
a jak víš, tak když krátíš musíš to zahrnout do výsledku.
Ale já rovnici výrazem 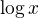 nekrátila ... anebo to prostě nikde nevidím...
nekrátila ... anebo to prostě nikde nevidím...
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#13 04. 11. 2010 09:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: A zase ty logaritmy
↑ zdenek1:
co já pro Tebe, vážený kolego neudělám, podobná varianta (1) byla zde- ale také s překlepem v zadání zřejmě.
Kdybych byla metodik SŠ, tak bych zadala úlohu 
Ovšem metodik SŠ nejsem a výchovný poradce také ne. Kde jsou zlaté časy, kdy logaritmovat před polednem se považovalo za zhůvěřilost (c).
Hodně zdaru celému týmu, je třeba uznat, že cíl "tazatele" je nesmírně ušlechtilý.
Offline
#15 04. 11. 2010 12:58
Re: A zase ty logaritmy
jelena napsal(a):
↑ zdenek1:
Kdybych byla metodik SŠ, tak bych zadala úlohu
Též metodikem nejsem, ale má přirozená ženská inteligence :D mne navedla na stejné řešení, viz výše, neboť by byla blbost, aby v zadání nebyl rovnou proveden součet dvou čísel (bez neznámé) pod odmocninou. :) Tímto zdravím veškeré ženské (=inteligentní) složení tohoto fóra. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#16 05. 11. 2010 10:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: A zase ty logaritmy
↑ gadgetka: omlouvám se, nevšimla jsem, že je přidána reakce na můj příspěvek.
gadgetka napsal(a):
přirozená ženská inteligence :D mne navedla na stejné řešení, viz výše...
takovou vlastnost nemám.
Použila jsem tlačítko Hledat (které je v horní liště vedle tlačítka Pravidla), jelikož jsem si vybavila, že takové zadání již bylo a opakovaně snad. Potom jsem použila Wolfram, ve kterém jsem prozkoušela možnou variantu vhodného zadání.
Že jsem si nevšimla, že řešení je již přidáno - sbírkové témata se špatně čtou. Navíc v příspěvcích není žádný komentář a pro nematematika je to čtení nezáživné. Navic nemáte ve zvyku si navzájem komentovat řešení, jako zde se neobjevilo, že podrobně a názorně popisuješ řešení od kolegy metamedika - taková má poznámka s odvoláním na jiné téma, které s předmětným nesouvisí, je proti netikete, jsem si toho vědomá, omluva.
---------------------------------------------------------------------------------------
K tématu 1 - nebylo odpovězeno:
gadgetka napsal(a):
Cheop napsal(a):
↑ gadgetka:
Krátila jsi celou rovnici výrazem log x
a jak víš, tak když krátíš musíš to zahrnout do výsledku.Ale já rovnici výrazem
nekrátila ... anebo to prostě nikde nevidím...
Je to k zadání: 
respektivě, řekl to ↑ zdenek1:, děkuji, ale řekla bych, že na SŠ to není dostatečně průhledné. Případně prosím kolegu Zdeňka o doplnění.
"Bezrizikové" odstranění stejných základů mocnin lze provést, pokud je základem mocniny číslo. Zde je ovšem základem promenná, proto postup kolegy ↑ Cheopa: - logaritmuje levou a pravou část (za předpokladu, že levá a pravá část jsou kladné) je více korektní. Druhá možnost je přepis na základ e - viz výklad od kolegy Mariana (a postup od kolegy Kondra o příspěvky výš).
Proto se u kolegy Cheopa neztratil jeden kořen.
Můj výklad je značně polopatický, bylo by dobré, aby k podobným "ne úplně jednoznačnám ulohám" se vyjadřoval někdo z odborně zdatných kolegů. Děkuji. Ovšem zda to odborně zdatný kolega najde ve sbirkové podobě, nevím.
Jak jsem uvedla, pro sebe nepovažuji za časově únosné lítat tady na koštěti po tématech a sjednávat alespoň základní dodržení pravidel. Je mi však lito, že neochota respektovat pravidla může vést k podobným nesrovnalostem.
Zdravím.
--------------
K tématu 2: úlohy jsou z Janečka.
Offline
#17 05. 11. 2010 12:26
Re: A zase ty logaritmy
Nevím, co na to říct ... snad jen tolik, že se mi tady na tom fóru přestává líbit. Chodila jsem sem ráda, ráda jsem pomáhala, vracela jsem se vzpomínkami na střední školu, od malička jsem taková, že když jsem něco věděla, nedokázala jsem držet pusu a stejné to je i s řešením příkladů. Nejsem na tomto fóru jediná, kdo příklady okamžitě řeší, bez nápovědy, ale tak nějak cítím z tvého příspěvku, jeleno, že je to hlavně narážka na mě. Nejsem génius, kolikrát v matice nadělám chyby, které by neudělal ani žák základní školy. Je to normální, nejsem robot, jsem jenom člověk. Byla jsem tedy ráda i za nakopnutí a rady, které jsem zde dostala ... před dvěma roky, než jsem sem přišla, jsem si pamatovala už jen základy středoškolské matematiky, dnes už si troufám i na integrály a derivace a sama mám radost, že umím zpátky to, v čem jsem byla kdysi opravdu výborná. Nevím, nějak se tu teď necítím vůbec dobře ... tak jsem se vypovídala a můžu jít ... chytrých lidí je tu hafo, blíží se zima, vezmu do ruky zase jehlice a klubíčka a budu užitečnější pro vlastní rodinu. Děkuji tomuto fóru za to, že mi dodal seběvědomí v tom, že něco opravdu znám ... zužitkuji to velmi záhy, otevřu si v našem malém městečku doučování a budu s láskou vzpomínat na fórum, kde mi bývalo tak dobře. A zcela určitě občas někdy nakouknu, abych viděla, jak se tu všichni máte ... ale že budu dodržovat pravidla, to ti, jeleno, radši neslíbím. Vím zcela určitě, že bych to nedodržela ... prostě jsem už taková. :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#18 05. 11. 2010 15:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: A zase ty logaritmy
↑ gadgetka:
děkuji za reakci.
Vlaďko, my se nerozumíme, což je snad normální.
A bohužel nemám moc času, abych napsala nějakou další slohovku na téma "Co podporujeme". O debatě k pravidlům jsem psala opakovaně - vyjádření (i třeba zamítavé) od Tebe nebylo. Proto navrhuji akceptovat to, co je uvedeno.
Případně, pokud chcete řešit automatově - otevřte debatu novou. Opakuji - není účelem, aby někdo odcházel a také není učelem, aby někdo se citil špatně.
Já se tady citím špatně dost často, potom si najdu pozitivum například v kolegyňce Marcele (Maca), která studuje dálkově - s rodinou, se zaměstnáním a začíná každý příspěvek tak, že je jasné, že nejdřív hledala, potom vloží své nápady a poprosí o pomoc. A potom si řeknu, že pořád to má smysl.
Nemám čas na předvádění, jak úžasně řeším kvadratickou rovnici, ale snad najdu čas na pomoc někomu, kdo si mou pomoc zasluhuji. Byť je to pomoc velmi skromná.
Doučování jsem po dlouhých letech praxe ukončila (skoro).
Vzájemná neúcta v tématech mi vadí - nedá se nic dělat, nejsem zkušena v online komunikaci. Je možné, že je to normální. Ohledně reagování na předchozí příspěvek jsem již prosila i kolegu Zdeňka.
Pro celý tým řešitelů v tomto tématu - pokud vynechám autora dotazu, tak průměrný věk v tomto tématu je cca 48 let. Pojďme si založit samostatné téma v Připomínkách, ať sestavu v takovém pokročilém věku nemusí rovnat tým Moderátoru značně mladších. Nebo, prosím, napíšte své vyjádření k příspěvku Pravidla. Děkuji Vám.
Omluva váženým Moderátorům k poznámce o věku.
---------------------------
část, která se tykala matematického dotazu k řešení rovnice, zřejmě není nijak aktuální.
Offline

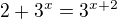



















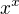 není prostá, takže z
není prostá, takže z  neplyne jenom
neplyne jenom 