Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 11. 2010 09:09
Dvojný integrál
Dobrý den, řeším teď příklady na dvojné integrály, ale mám trochu problémy s určováním mezí:
př1.:
na množině 
převedl jsem dó polárních souřadnic a vznikly mi meze takto:
a dále upravil na tento tvar (mohu to takto upravovat? zdá se mi to totiž příliš snadné):
 a z tohoto jsem to integroval dále...
a z tohoto jsem to integroval dále...
př2.:
Zde nevím zda mám dobře určené meze:
na množině 
převedl jsem dó polárních souřadnic a vznikly mi meze takto:
Děkuji za radu, a ještě bych se rád zeptal na jednu věc; výpočet integrálu kontroluji pomoci programu Maple a nevíte, zda umí i vypočítat meze, popřípadě kde by byla na internetu nějaká ukázka, jak se to zadává. Kontrolu výpočtu integrálu provádím až na mezích, které já sám vypočtu a v momentě, kdy špatně určím meze, bude i integrál samozřejmě špatný, takže bych rád kontroloval i výpočet mezí.
Díky
Offline
#7 05. 11. 2010 12:27
#9 05. 11. 2010 13:50
Re: Dvojný integrál
↑ NetFenix:
Neznám podrobnosti z Tvého výpočtu per partes, ale tato metoda zde není tou nejvýhodnější, zatímco
o substituci  si integrál
si integrál  přímo říká, neboť pak
přímo říká, neboť pak 
a dostáváme  (až na integreční konstantu) ,
(až na integreční konstantu) ,
derivováním se snadno přesvědčíme, že  .
.
Offline



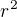




 .
.

 jsou na sobě nezávislé můžeme psát:
jsou na sobě nezávislé můžeme psát:



