Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s exponencialnymi clenmi (TOTO TÉMA JE VYŘEŠENÉ)
#3 31. 10. 2010 21:58
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: limita s exponencialnymi clenmi
pro kontrolu: ta nejrychlejsi exponenciale tam je dvakrat, v citateli je trosku zamaskovana.
Offline
#6 06. 11. 2010 15:29
Re: limita s exponencialnymi clenmi
predelil som kazdy vyraz 9**n avsak nie som si isty ci sa bude kazdy predeleny vyraz rovnat nule , napr problem mam pri n**2*7**n /9**n sice 9**n je viac ako 7**n ale vsak v citateli je sucin , takze to by bolo potom nekonecno na 2 krat 7 **n , ALEBO by sme "vykratili" 7**n s 9**n ? ale i tak to pojde do nekonecna vdaka n**2 ... a vo vyrazoch v citateli podobne ...sice vyslo v prvom vyraze 3 a v poslednom vyraze s menovatela 5 , ale ostatok idu bud k 0 alebo k nekonecnu takze
nekonecno / nekonecno ...
Offline
#12 06. 11. 2010 21:43
Re: limita s exponencialnymi clenmi
tak ja uz ozaj neviem ked to predelim ... vsak tam ostanu tie vyrazy v citateli n a v menovateli 2n+1 tak limita neexistuje ? :) a co keby som tu aplikoval l hospitalovo pravidlo ? ale neda sa t ouniverzalne pouzit ... ze ?
Offline
#16 07. 11. 2010 11:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s exponencialnymi clenmi
↑ vysoka:
ke kterému výsledku daleko? K výsledku ověřenému v online nástrojích úvodního tématu VŠ?
každý člen jsem dle předchozích pokynů kolegů (zejména kolegy Stýva, děkuji) kratila n*(-2)^(5n). Tedy "zajimavé" jsou pouze prostřední sčítanec v čitateli a prostřední sčítanec v jmenovateli.
Je to v pořádku? Děkuji.
Offline
#17 07. 11. 2010 13:28
Re: limita s exponencialnymi clenmi
v ktorom nastroji konkretne ? na vypocet limity nebol konkretne uvedeny akurat integraly ... a ked so mdal v google tak naslo jedenej nefunkcni
avsak stale to vychodaza 1 / 2 ?
a v moznych odpovediach
a -1/4
b 1/5
c neexistuje
d 0
e - nekonecno
f 1/4
taky vysledok nie je ?
Offline
#18 07. 11. 2010 14:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s exponencialnymi clenmi
↑ vysoka:
konkrétně - v tom tématu, co je natřeno na červeno. V 1. zprávě jsou odkazy, v 2. zprávě jsou příklady matematických výpočtů - zvolit Calculus a Analysis.
Jak se upravil tento zápis v jmenovateli 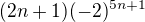 , aby se dálo bez problemu vydělit
, aby se dálo bez problemu vydělit 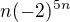 ?
?
Děkuji.
Offline
#20 07. 11. 2010 15:49
Re: limita s exponencialnymi clenmi
no vsak ked je jednicka v exponentu tak sa to da prepisat ako (-2) takze k tym clenom v tom sucine pribudne tento ...
a tak tym padom ked predelime spominanym vyrazom ... tak vyjde (-2) *(2 - (1/ n)) teda -4 .... takze ak som neurobil chybu so znamienkom tak by to mal byt vysledok -1/4
Offline
#21 07. 11. 2010 16:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s exponencialnymi clenmi
↑ vysoka:
ano, myslela jsem takovou úpravu 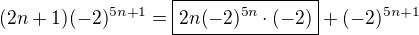 to, co je v krabičce, je to, co dává v celkovém výsledku -1/4.
to, co je v krabičce, je to, co dává v celkovém výsledku -1/4.
Výsledek od stroje.
V pořádku?
Offline
#22 07. 11. 2010 16:46
Re: limita s exponencialnymi clenmi
ano , aspon som uz zistil kde mam chybu ... som zabudol na tu jednicku a preto mi to inac vychadzalo ... ale aj tie online nastroje su fajn ...nie vzdy , ale tiez zabehu hodne casu ked kym to tam clovek zada ... taktiez aj ten tex ... ale dik ze sme sa k tomu spolocne dopracovali
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s exponencialnymi clenmi (TOTO TÉMA JE VYŘEŠENÉ)


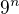
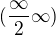 ( 1nekonecno / 2 nekonecna ) dobre ?
( 1nekonecno / 2 nekonecna ) dobre ?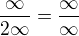 není definovaný výraz
není definovaný výraz