Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s prirodz logaritmom (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 11. 2010 12:42
limita s prirodz logaritmom
0
1
2
3
PI
nekonecno
vyslo mi podiel logaritmov kedze je tam minus ... a to je pri n iducom do nekonecna rovna 1 a tak ln 1 sa rovna 0 , avsak neviem ci su to legalne upravy lebo vyzera ze je t o nespravne
Offline
- (téma jako vyřešené označil(a) vysoka)
#8 09. 11. 2010 09:25 — Editoval Rumburak (09. 11. 2010 09:30)
Re: limita s prirodz logaritmom
Tak podrobněji: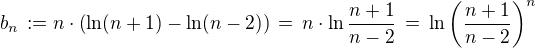
... tato úprava využívá pouze základních vlastností obecné logaritmické funkce.
Dále: 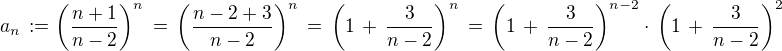 .
.
Odtud je zřejmé, že 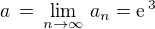 a
a 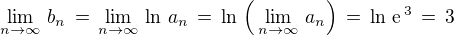 .
.
Záměna pořadí limity a logaritmu je přípustná na základě spojitosti logaritmu v bodě  .
.
Ale jak jsi k výsledku dospěl Ty , to ani já nevím. :-)
Offline
#9 11. 11. 2010 09:35
Re: limita s prirodz logaritmom
dostal som sa k vysledku tak, ze som skusal postupne vsetky moznosti a ked mi dalo sparvne pri 3 , tak som bol happy , aj ked som za to samozrejme ziskal zlomok bodov co som mohol ziskat kedze so mto nezaskrtol na prvy krat spravne ... :) a este bola odpoved PI teda to je blizke 3, takze niekoho aj to mohli nabadat ze to niekde tam bude sa pohybovat :) diky za pomoc
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s prirodz logaritmom (TOTO TÉMA JE VYŘEŠENÉ)
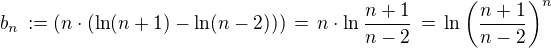 .
.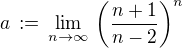 , pak ke hledané limitě
, pak ke hledané limitě