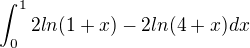Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 11. 2010 10:11
Trojný integrál
Zdravím, mám problém při řešení integrálu, protože mi tam vychází stále záporný logaritmus, přesto však když příklad zadám do maplu, tak ho spočte v pohodě, ale když pak dělám postupné integrace, tak se shodují s mým postupem, tak nevím...
Zadání:
Můj postup:![kopírovat do textarea $\int_{0}^{1}\int_{2}^{5}\int_{2}^{4}\frac{1}{1-x-y}dzdydx = \int_{0}^{1}\int_{2}^{5}[\frac{z}{1-x-y}]_{z=2}^{z=4}dydx =$](/mathtex/b0/b06f3972a52a421fd1a52f81bb33f007.gif)
![kopírovat do textarea $\int_{0}^{1}\int_{2}^{5}[\frac{2}{1-x-y}]dydx = \int_{0}^{1}[2ln(1-x-y)]_{y=2}^{y=5}dx =$](/mathtex/d7/d7f0b3050eee05474fde96b7ad8c93a9.gif)
 ....
....
a nakonec mi tam už stejně ten zápor zůstane
A ještě jsem se chtěl zeptat jak určovat meze u trojných integrálů, když mám třeba množinu:
Tak spodní meze budou nuly to je asi jasný, a teď ty horní mi vychází z té poslední podmínky:
z = 1-x-y
y = 1-x-z
x = 1-y-z
což asi není na první pohled dobře... Díky za rady
Offline
#2 11. 11. 2010 11:12 — Editoval Rumburak (05. 01. 2016 10:52)
Re: Trojný integrál
Jádrem úlohy je vypočítat integrál 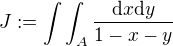 , kde
, kde ![kopírovat do textarea $A=[0,\,1]\times[2,\,5]$](/mathtex/1e/1ef785dc28464db62565722568cf6ca5.gif) .
.
Integrovaná funkce nabývá na množině A pouze záporných hodnot, proto integrál bude mít zápornou hodnotu.
Ale pozor na to, že primitivní funkce k funkci 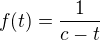 je
je 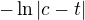 (v libovolném intervalu neobsahujícím bod
(v libovolném intervalu neobsahujícím bod ![kopírovat do textarea $[c]$](/mathtex/69/696b805d6a06c88e67cfc7c81f5ceb72.gif) ).
).
Ke druhému dotazu:
Možina M by správně po formální stránce měla být vyjádřena takto: ![kopírovat do textarea $M=\{[x,y,z]\in\mathb{R}^3\,;\, x\ge \,0 \,\wedge\, y\ge 0 \,\wedge \,z\ge0 \,\wedge \,x+y+z\le 1\}$](/mathtex/27/277a59a292669fcc5501a1499a9dce4b.gif) .
.
Ten přechod od vícerozměrných integrálů k méněrozměrným by měl být vysvětlen v kapitole o Fubiniově větě - možných způsobů,
jak postupovat, je více.
Ukážeme si jednu možnost.
V prvé řadě si určíme kolmý průmět množiny M do některé souřadnicové rovniy. Volbu té souř. roviny provádíme s ohledem na
početní výhodnost, což ale zde nebude hrát roli, protože podmínka určující množinu M je vzhledem k proměnným x,y, z symetrická.
Zvolme si tedy třeba rovinu "xy" a hledejme kolmý průmět množiny M do této roviny. Pomocí určité geometrické představivosti
a volby z = 0 snadno zjistíme, že hledaným průmětem je množina
![kopírovat do textarea $T=\{[x,y]\in\mathb{R}^2\,;\, x\ge \,0 \,\wedge\, y\ge 0 \,\wedge \,x+y\le 1\}$](/mathtex/09/09a4c191c4479c7c7aa247f0662356be.gif) .
.
Volbou bodu [x, y] této množiny a z podmímek na body množiny M obržíme podmínku 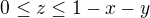 pro hodnoty souřadnice "z".
pro hodnoty souřadnice "z".
Fubiniova věta pak dává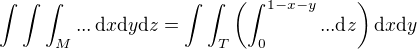
a analogicky dále.
Offline
#5 11. 11. 2010 11:48
Re: Trojný integrál
"Jsou dány dvě kružnice, z nichž jedné kouká z kapsy bagr."
Offline
#6 11. 11. 2010 11:52
Re: Trojný integrál
↑ NetFenix:
že by absolutni hodnota 2ln(|-x-1|)-2ln(|-4-x|) = 2ln(x+1)-2ln(4+x) ....
"Jsou dány dvě kružnice, z nichž jedné kouká z kapsy bagr."
Offline
![kopírovat do textarea $\int_{0}^{1}\int_{2}^{5}[\frac{2}{1-x-y}]dydx = - \int_{0}^{1}[2ln(1-x-y)]_{y=2}^{y=5}dx =$](/mathtex/85/85d45c56fdbd6e11e7d42b766cb07d20.gif)