Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 04. 2008 16:10
objem kužele a povrch kužele
Ahoj,
nutně potřebuju pomoct s výpočtem následujících příkladů:
1)
Povrch kužele je 235,5 cm2, osový řez je rovnostranný trojúhelnik. Vypočtěte objem kužele
2)
Objem kužele je 1000 mm3, obsah osového řezu je 100 mm2. Vypočtěte povrch kužele.
Výsledky:
[1] 226,6 cm3
[2] 711,65 mm2
Díky za každou radu a pomoc
Offline
#2 19. 04. 2008 16:50
Re: objem kužele a povrch kužele
↑ sustr:
ad 1)
objem kužele 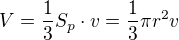 , kde r je polomer kruzice, ktera tvori podstavu a v je vyska
, kde r je polomer kruzice, ktera tvori podstavu a v je vyska
povrch kužele 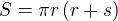 , kde r je polomer a s je delka bocni strany.
, kde r je polomer a s je delka bocni strany.
Naznacim ti kroky, upravy a odvozeni zkus sam nebo napis ;-)
Nakresli si rovnostranny trojuhelnik, ktery je stredovym rezem kuzele a vyznac sem i vysku kuzele v. Z toho rovnostranneho trojuhelniku vychazi, ze delka bocni strany s je rovna prumeru podstavy, tj. 2r.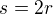 ...tohle dosad do vzorce pro povrch a zustane ti tam jednina neznama r (kterou vyjadris nakonec ve tvaru
...tohle dosad do vzorce pro povrch a zustane ti tam jednina neznama r (kterou vyjadris nakonec ve tvaru  )
)
Nakresleny stredovy rez pouzij jeste pro vypocet vysky, kterou urcis podle Pythagorovy vety z trojuhelniku s preponou s = 2r a odvesnami r a v...takze pro vysku urco najdes vztah: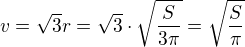
Dosadis do vztahu pro objem...za r a v odvozene vztahy a dostanes: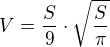
po dosazeni mas vysledek
Offline