Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 11. 2010 20:51
Geometrické úlohy
Pěkný večer vám všem přeji,
pomohli byste mi, prosím, s vyřešením těchto příkladů? Pokusil jsem se s nimi poprat sám, ale částečně neúspěšně u prvních dvou a naprosto neúspěšně u ostatních. Potřeboval bych, jestli byste mi vysvětlili princip, jak tyto úlohy řešit. Konečné výsledky mám.
1. Vzdálenost tětivy od středu kružnice je 6 cm, příslušný středový úhel má velikost 60 stupňů. Vypočítejte obsah kruhové výseče.
(Zde jsem to vypočetl víceméně sám, ovšem výsledkem je přesně 8pí a já mám 7,9pí... takže by mě spíše zajímalo, jak tuto úlohu řešit obecně. Dělal jsem to tak, že jsem si vypočetl tu stranu, která symbolizuje poloměr kružnice, pomocí cosinu 30 stupňů. a to pak dosadil do vzorce pro kruhovou výseč, tedy úhel*pí*r*r/360 a vyšlo mi to co mi vyšlo...)
2. Vypočítejte poloměr kružnice, jejíž délka je o 7cm větší než obvod pravidelného šestiúhelníku, který je této kružnici vepsán.
(Zde jsem se snažil udělat rovnici, ze které bych poté vyjádřil poloměr. Přibližně něják takto 2*pí*r + 7 = 6*((sin30*r)*2) ovšem vyšla mi naprostá blbost.)
3. Do kružnice je vepsán čtyřúhelník ABCD tak, že poměr délek oblouků AB, BC, CD, DA je 2 : 3 : 3 : 4. Vypočítejte velikosti jeho vnitřních úhlů a poměr délek jeho stran.
4. Trojúhelník ABC má obvod 100cm, jemu podobný trojúhelník A'B'C' má strany o 8cm, 14cm, 18cm větší, než jsou strany trojúhelníku ABC. Vypočítejte délky stran obou trojúhelníků.
5. Odvěsna pravoúhlého rovnoramenného trojúhelníku má délku 4cm. Vypočítejte obsah obrazce ohraničeného kružnicí trojúhelníku vepsanou a kružnicí trojúhelníku opsanou.
(U těchto 3 posledních příkladů si nevím vůbec rady...)
Děkuji již dopředu za námahu a za pomoc!
[Neznámý: Až keď je dostatočná tma, vidno hviezdy...]
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 20. 11. 2010 20:58
Re: Geometrické úlohy
↑ Měsíček:
2)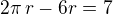
pro délku strany pravidelného šestiúhelnku platí, že je stejná jako
poloměr kružnice opsané tomuto šestiúhelníku (což je náš případ)
Offline
#3 20. 11. 2010 21:01
Re: Geometrické úlohy
↑ Měsíček:
Protože 60° je šestina plného úhlu 360°, bude obsah výseče roven 1/6 obsahu kružnice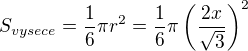
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 20. 11. 2010 21:25
Re: Geometrické úlohy
↑ Měsíček:
5) Střed kružnice opsané je ve středu přepony a poloměr je polovina přepony 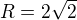 (přeponu vypočítáš z Pyth. věty)
(přeponu vypočítáš z Pyth. věty)
TAkže obsah kružnice opsané je 
Potřebujeme poloměr kružnice vepsané  .
.
Z obrázku je 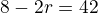 (přepona)
(přepona)
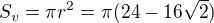
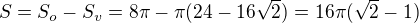
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 20. 11. 2010 21:28 — Editoval BakyX (20. 11. 2010 22:37)
Re: Geometrické úlohy
3. Pre dĺžku kružnicového oblúku platí ,
,
kde uhol je vlastne príslušný stredový uhol oblúku. Označme stredové uhly po rade ako uhly štvoruholníka s čiarou a dajme do pomeru dĺžky oblúkov:
Vidíme, že pomer dĺžok oblúkov je rovný pomeru veľkosti stredových uhlov. Na základe toho, že súčet týchto uhlov je 360, učíme ich veľkosti: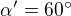


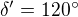
Označme si v štvoruholníku stred kružnice opísanej S. SA=SB=SC=SD. V trojuholník ASB, BSC, CSD, DSA vieme vypočítať vnútorne uhly na základe jedného uhla a rovnoramennosti. Na základe týchto uhlom vidíme, že: 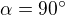

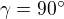
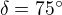
Stred strany AB označme P. Keďže stred kružnice opísanej leží na priesešníku osí strán, tak trojuholník APS je pravouhlý s pravým uhlom pri vrchole P. Keďže trojuholník ABS je rovnoramenný, tak uhol ABS je úsečkou PS rozdelený na dve polovice. Vyjadríme sínus tohto uhla:
Ostatné strany dostaneme analogicky. Dáme ich do pomeru:
Dosadíš, vypočítaš sínusy a máš výsledok. Rozumieš postupu ?
1^6 - 2^6 + 3^6 = 666
Offline
#6 20. 11. 2010 21:33 — Editoval BakyX (20. 11. 2010 22:17)
Re: Geometrické úlohy
4. Ak sú trojuholníky podobné, tak pre ich strany platí:
Strany a', b', c' sú strany väčšieho podobného trojuholníka. Z hornej rovnosti sa da vyvodiť, že: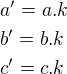
V zadaniu máme vyjadrené strany podobného trojuholníka pomocou strán menšieho trojuholníka: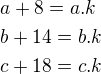
Sčítame všetky tri rovnice:
Dosadíš, dopočítaš strany oboch trojuholníkov a máš výsledok
1^6 - 2^6 + 3^6 = 666
Offline
#8 20. 11. 2010 22:36
Offline
#11 21. 11. 2010 11:59 — Editoval Chrpa (23. 11. 2010 09:39)
Re: Geometrické úlohy
↑ Měsíček:
Obrázek napoví?
Pro výpočet délek stran čtyřúhelníku použij kosinovou větu (popřípadě větu starého Pythágora)
Offline

