Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 04. 2008 15:51
Re: obor hodnot funkce
Neznám nějaký obecný postup, jak určit obor hodnot funkce… Leda celkově vyšetřit její průběh (asymptoty, monotónnost atd).
Toto bych řešil takovou jednoduchou úvahou… Vidím, že funkce f je sudá, omezím se tedy jen na  . V nule nabývá funkce hodnoty nula, pro jakékoliv vyšší je funkční hodnota vyšší a vzhledem k tomu, že logaritmická funkce má obor hodnot všechna reálná čísla, nejsme tady shora nijak ohraničeni. Obor hodnot tedy je
. V nule nabývá funkce hodnoty nula, pro jakékoliv vyšší je funkční hodnota vyšší a vzhledem k tomu, že logaritmická funkce má obor hodnot všechna reálná čísla, nejsme tady shora nijak ohraničeni. Obor hodnot tedy je 
Offline
#3 23. 04. 2008 22:11 — Editoval Jorica (23. 04. 2008 22:12)
Re: obor hodnot funkce
Aby se nemusel vysetrovat cely prubeh funkce, je mozne stanovit funkci inverni a u ni najit definicni obor (na to uz algoritmy jsou).
Zadana funkce  neni prosta, proto vyjde jako inverzni funkce:
neni prosta, proto vyjde jako inverzni funkce: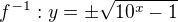 .
.
Hledam-li definicni obor techto inverznich funkci, pro obe plati, ze ze musi byt splnena podminka: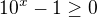
Odtud po doreseni exponencialni nerovnice plati, ze  .
.
Obor hodnot puvodni funkce  je roven definicnimu oboru inverzni funkce
je roven definicnimu oboru inverzni funkce  , takze:
, takze:
Offline
