Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 11. 2010 09:39
Kombinatorika, zadání č. 5
Určete všechna dvojciferná přirozená n, pro která platí, že n3-n je dělitelné číslem 100.
Poznámka: Využijte kombinatorické úvahy, rozhodně nemáte dosazovat 90 různých hodnot!
Přišel jsem na toto:
n^3-n je dán součinem tří po sobě jdoucích celých čísel ---> n^3-n = n * (n^2 - 1) = n * (n+1) * (n-1) = (n-1)(n)(n+1)
Tudíž to znamená že jedno z nich musí být násobkem tří a z toho vyplývá že násobek těchto tří čísel musí být dělitelný 3. To ale znamená že musí být tento násobek dělitelný i 6 protože šestka je násobkem 3.
Další postup mi ale není jasný, stále i tak mi zbývá mnoho čísel.....
Nějaký nápad?
Offline
#2 23. 11. 2010 10:31
Re: Kombinatorika, zadání č. 5
Uvažoval jsem o rozdělení čísla 100 ---> 100 = 4*25 = 2*2*5*5. Čímž mě napadlo že dané čísla musí být také dělitelná dvěmi a zároveň čtyřmi (budou sudá- 12, 16, 20, 24....je jich mnoho:-( a né všechny jsou řešením), a také to mohou být čísla, která jsou dělitelná pěti a zároveň dvacetipěti(budou lichá - zde jsou pouze dvě a pasují jako výsledek :-) )
Nicméně mi stále nevyhovuje spoustu čísel a zatím mě nenapadá nic jak na to přijít.... :-(
Offline
#4 23. 11. 2010 10:55
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Kombinatorika, zadání č. 5
↑ maniaX: Čísla 4 a 25 jsou dobrá cesta, stjně tak rozklad (n-1)n(n+1). Poslední dílek skládačky je Čínská zbytková věta.
↑ Cheop: To není správně.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#8 24. 11. 2010 01:48
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Kombinatorika, zadání č. 5
↑ maniaX:Ze zbytku n po dělení 25 a zbytku n po dělení 4 umíme určit zbytek n po dělení 100. To nám spolu s informací, že n je dvojmístné, dává dostatek informací.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#9 24. 11. 2010 09:26
Re: Kombinatorika, zadání č. 5
↑ Kondr: Pokud vezmu v úvahu číslo n=25, které mi vyhovovalo v rozkladu (n-1)n(n+1). Tak zbytek po dělení 25 je 0, zbytek po dělení 4 je 1. Jak jsem z tohoto schopen zjistit zbytek po dělení 100? Přičemž vím že 25 mod 100 = 25
Jsem ted z toho zmatený.
Offline
#11 27. 11. 2010 12:34 — Editoval Kondr (27. 11. 2010 12:36)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Kombinatorika, zadání č. 5
↑ petrkovar: Zbytek po dělení 100 čísla n je n, a to je přesně to, co chceme určit, ne?
↑ maniaX:Nebereme v úvahu n, ale možné zbytky n mod 25 a n mod 4 (každý nezávisle) a z nich teprve chceme n vypočítat.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#12 27. 11. 2010 16:04
- Mathematic
- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Kombinatorika, zadání č. 5
chcu se zeptat, jak ste přišli na to že ty čísla musí končit číslicí (1,4,5,6,9)...
a aby n^3 - n končlo 0, tak je více možností, protože to může končit (0, 1, 4, 5, 6, 9) jen v případě, když to končí 0, tak vyjde číslo s jednou nulou na konci, jenže v zadání je dělit 100, čili to musíme ošetřit tak aby to vyhovovalo tak, aby výsledný součin měl poslední 2 číslice 0. já to zkoušel jen dosazovat, takže moc netuším, jaký vzorec jste pro to použili, aby vám vyšly právě ty čísla bez té 0.
Offline
#14 28. 11. 2010 20:05
Re: Kombinatorika, zadání č. 5
Co si myslíte o tomto výpočtu ?
2-ciferné číslo xx*3 -> xxx
(99 max) (99*3=297 je max)
3*n - n
xxx - xx
(297-99=198) -> jen 100 samotné nikoliv násobky takže řeším jen neznámou v úloze
3*xx - xx = 100
3*n - n = 100
2*n = 100
n = 50
Offline
#15 28. 11. 2010 20:38
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Kombinatorika, zadání č. 5
↑ bereline: Toto by byl korektní výpočet (byť nedostatečně komentovaný) pro výraz n*3-n. My máme v zadání n^3-n, lépe zapsáno 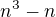 .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#20 29. 11. 2010 22:51
Re: Kombinatorika, zadání č. 5
Zdravím,
po dlouhém boji jsem tento způsob řešení snad pochopil, za což děkuji zde přítomným. Problém mám pouze s tím, že v zadání je poznámka, aby jsme využili kombinatorické úvahy, což podle mě případ s čínskou zbytkovou větou není. Nemáte zde prosím nápad jak toto řešit pomocí kombinatoriky?
Děkuji
Offline
#21 02. 12. 2010 12:23
Re: Kombinatorika, zadání č. 5
No já uvažoval tímto způsobem:
nejpve n^3-n=(n-1)n(n+1) cože je posloupnost předchozí vybrané a následující číslo
dále stačí když dvě z těchto čísel dají při násobení výsledek dělitelný 100, pak už ať násobíme čím chceme 100*n bude vždy dělitelné stovkou
dál se musíme logickky zamyslet která dvojciferná čísla..po již zmíněném rozkladu 100 = 4*25 = 2*2*5*5
protože mi stačí 2 čísla skusím je tedy složit z tohoto rozkladu(2,2,5,5):
a)2*5=10; 2*5=10
b)2*2*5=20; 5=5
c)5*5=25; 2*2=4
d)2*5*5=50; 2=2
e)2*2*5*5=100 a jakékoliv celé číslo
Protože máme tři po sobě jdoucí čísla (n-1)n(n+1) nemůže nastat aby, jakékoliv dvě čísla trojce byla obě dělitelná současně viz a)10 a 10
viz b)20 a 5 ...např20,21,23... ale na 25 se uz nelze dostat
Pak tedy můžeme najít dvojciferná celá čísla pro které platí že z tří po sobě jdoucích čísel je jedno dělitené 25 a další 4?
Pak tedy můžeme najít dvojciferná celá čísla pro které platí že z tří po sobě jdoucích čísel je jedno dělitené 50 a další 2?
Pak tedy můžeme najít dvojciferná celá čísla pro které platí že z tří po sobě jdoucích čísel je jedno dělitené 100?
Důežité je nezapomenout že DVOJCIFERNÉ musí být JEN ČÍSLO n V (n-1)n(n+1)
P=NP >)
Offline
#23 02. 12. 2010 16:54
Re: Kombinatorika, zadání č. 5
Ano, tudy přibližně vede cesta.
Samozřejmě si můžete dosažené řešení ověřit hrubou silou, ale v projektu jsou hodnocené právě kombinatorické úvahy, nikoliv excelovské tabulky a podobné "bezmyšlenkové" postupy.
Myslím, že příspěvek ↑ Drakee: je na hranici, za kterou bychom při publikování dílčích výsledků na tomto fóru už neměli jít.
Offline
#24 02. 12. 2010 17:29
Re: Kombinatorika, zadání č. 5
Bohužel v praxi dostává zaplaceno ten kdo s výsledkem příjde dříve.... a pro programátora je snažší napsat 5 řádků kódu cyklu s jedním porovnáním, což zabere asi minutu... než 2 hodiny vymýšlet algoritmus pouze pro zjištění čísel daných vlastností a poté ho iplementovat. :( bohuzel smutná tvrdá ruka trhu
P=NP >)
Offline
#25 03. 12. 2010 10:06
Re: Kombinatorika, zadání č. 5
↑ Drakee:Toto je jen projekt do DIM. Tady trénujeme - ne však programování, od toho jsou zase jiné předměty.
Úlohy v reálu bývají často mnohem komplikovanější než náš projekt za 10b a bez teoretického rozboru je iluzorní, že be se počítač kdy k řešení mohl dobrat. Za svou krátkou kariéru jsem řešil několik úloh z praxe, kde přístup hrubou silou prostě nebyl možný kvůli fenoménu kombinatorické exploze.
Jak by si programátor poradil třeba s tímto problémem?
Zkuste si rozmyslet, jak by si váš kód poradil s naší úlohou, když nebudeme mít dvojciferná, ale patnácticiferná čísla? Jak moc se změní teoretický rozbor?
Offline