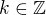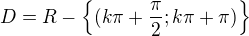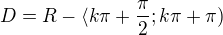Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 12. 2010 18:15
definičný obor funkcie
Ahojte,
Znenie ulohy: Urcte definicny obor funcie : 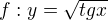
POdla mna to je D(f)=(2k+1)*pi/2 , je to spravne? lebo toto plati pre klasicku y=tgx funkciu ale kedze hodnota x hodnot sa nemeni tak by to malo platit aj pre tuto ulohu.
Offline
- (téma jako vyřešené označil(a) faktorial)
#2 03. 12. 2010 18:28
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: definičný obor funkcie
(Cituji tě, protože jsi po sobě dřív mazal.)
faktorial napsal(a):
Ahojte,
Znenie ulohy: Urcte definicny obor funcie :
POdla mna to je D(f)=(2k+1)*pi/2 , je to spravne? lebo toto plati pre klasicku y=tgx funkciu ale kedze hodnota x hodnot sa nemeni tak by to malo platit aj pre tuto ulohu.
1. Definiční obor není číslo, ale množina čísel.
2. Body, které se snažíš zapsat do definičního oboru, v něm právě nebudou.
3. Navíc musíš vyšetřit, kdy je argument odmocniny nezáporné číslo. Kdyby totiž tangens vyšel záporný, neumíme ho pak odmocnit.
Offline
#3 03. 12. 2010 18:51
Re: definičný obor funkcie
↑ BrozekP:
zabudol som malo by to byt: D(f)=R-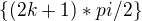 a podla 3.bodu: D(f)=R-
a podla 3.bodu: D(f)=R-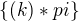 kde k je cele cislo, teraz je to dobre?
kde k je cele cislo, teraz je to dobre?
Offline
#4 03. 12. 2010 19:09
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: definičný obor funkcie
↑ faktorial:
Ne, na jistých intervalech je tangens záporný. Kdy je  ?
?
Offline
#6 03. 12. 2010 20:47
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: definičný obor funkcie
↑ faktorial:
Víš jak vypadá graf funkce tangens? Je funkce záporná pouze v izolovaných bodech (jak píšeš), nebo na intervalech? Zkus najít intervaly, kde je kladná.
Offline
#7 04. 12. 2010 08:33 — Editoval faktorial (04. 12. 2010 08:48)
Re: definičný obor funkcie
viem ako vypada funkcia tg. ja som mal na mysli interval PI/2 az PI, nemyslel som to ako izolovane body. Tak tg je kladna na <0,PI/2) potom zase PI az 3PI/2.
to co som napisal je uplne zle alebo nieco je aj dobre natom?
da sa ten definicny obor aj nejako matematicky vypocitat?
Offline
#10 07. 12. 2010 18:07
Offline
#12 09. 12. 2010 21:33
Re: definičný obor funkcie
↑ faktorial:
No dá, ale nezdá se ti to zbytečně složitý?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#15 14. 12. 2010 12:39
Offline


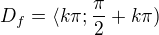 ,
,