Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 14. 12. 2010 21:32
Re: Přechodový děj
↑ kotry:
a) i(-0)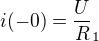 je správně.
je správně.
Před rozepnutím spínače je proud tekoucí indukčností stejný jako proud tekoucí zdrojem.
b) i(oo)
Zde už není jedno, zda vypočítáme proud tekoucí zdrojem, nebo proud tekoucí indukčností. To, co jsi vypočítal, je proud tekoucí zdrojem. Proud tekoucí indukčností by měl být 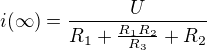 .
.
c) i(t)
Doporučuji nejdřív levou část obvodu (U0, R1, R3) zjednodušit podle Théveninova teorému
Další postup pak znamená řešit standardní sériový RL obvod s počáteční podmínkou, kterou už známe z bodu a).
Ve standardním RL obvodu bude 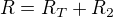 ,
,  .
.
Offline
#4 20. 12. 2010 15:38
Re: Přechodový děj
↑ kotry:
V sériovém obvodu RL platí:
Po dosazení z definičních vztahů pro indukci a odpor:
Obecné řešení této dif. rovnice: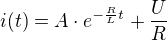 ,
,
kde konstantu  zjistíme z počáteční podmíky pro
zjistíme z počáteční podmíky pro 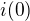 :
:
Jak už jsem psal dřív, za R a U je třeba dosadit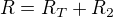 ,
,  .
.
Poznámka:
Jak je vidět, stačí ti znát hodnotu i(0-). Ty ostatní (i(nek), u(nek, atd.) jsou obsaženy v řešení dif. rovnice.
Offline
#6 21. 12. 2010 07:04
Re: Přechodový děj
↑ kotry:
Ne, pro t=0 ani pro t=oo to nedává správné hodnoty.
Do vztahu 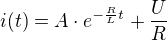 postupně dosaď
postupně dosaď
za  ,
,
za 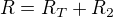 ,
,
za 
a nakonec za  a
a  to, co jsi vypočítal jako Théveninovu ekvivalentní substituci.
to, co jsi vypočítal jako Théveninovu ekvivalentní substituci.
Umíš vypočítat  a
a  ?
?
Výsledek by měl být  ,
,
kde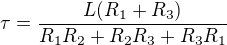 ,
,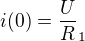 ,
,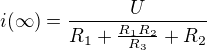 .
.
Offline
#7 21. 12. 2010 16:08
Re: Přechodový děj
↑ medvidek:
Thevenin:
I2= Ut/(Rt+R2) PROUD přes R2 a L
I1=U/(R1+R3) PROUD náhradního obvodu (tedy bez větve R2,L)
Ut=U3=R3*I1 Napětí na R3
Rt=(R1*R3)/(R1+R3) ODPOR náhradního obvodu- tam kde byla původně větev R2,L
Ut=I2*(Rt+R2) napětí na: R2, L
i(t)= i(0)+i(00)
i(t)= (U/R1 - U/(R1+(R1*R2)/R3+R2) ) * e^(-t/tau) + U/(R1+(R1*R2)/R3+R2) )
takhle je to už dobře ??
doufam že je to alespoň drobet srozumitelný...
Offline
#8 21. 12. 2010 19:09 — Editoval medvidek (21. 12. 2010 21:03)
Re: Přechodový děj
↑ kotry:
Chvíli mi trvalo pochopit ty slovní popisy, ale nakonec mohu souhlasit.
Všechny vztahy jsou dobře až na tento i(t)= i(0)+i(00). Vlevo je proměnná, vpravo konstanta. Nejjednodušší je ho vynechat.
Jinak rozdíl i(0)-i(00) bychom mohli nazvat celkový úbytek proudu i(t) v důsledku přechodového děje.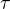 je relaxační (nebo také charakteristická) doba přechodového děje (obecně jakéhokoli exponenciálního procesu). Je to doba, během které dojde k většině změn proudů a napětí (až na 1/e-tou část celkové změny).
je relaxační (nebo také charakteristická) doba přechodového děje (obecně jakéhokoli exponenciálního procesu). Je to doba, během které dojde k většině změn proudů a napětí (až na 1/e-tou část celkové změny).
EDIT:
Oprava: místo o rozdílu i(0)-i(00) jsem výše psal o součtu.
Offline
#10 21. 12. 2010 19:46 — Editoval medvidek (21. 12. 2010 19:48)
Re: Přechodový děj
↑ kotry:
Výsledek platí pro všechna  .
.
Proměnná  patří do výsledku tak jak je. Pro t=0 vychází velikost proudu na začátku děje, v limitě t=oo vychází velikost proudu na konci děje, například pro t=5 dostaneme velikost proudu na konci páté sekundy.
patří do výsledku tak jak je. Pro t=0 vychází velikost proudu na začátku děje, v limitě t=oo vychází velikost proudu na konci děje, například pro t=5 dostaneme velikost proudu na konci páté sekundy.
EDIT:
Závislost 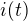 pak můžeš vynést do grafu.
pak můžeš vynést do grafu.
Offline
