Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 01. 2011 13:31
Logaritmická rovnice
Zdravím Lidičky, počítám zrovna logaritmy a nejsem si jist, zda u této rovnice postupuji správně ?!?
koukněte a poraďte mi prosím...
Všichni se v něčem předstihujeme, proto se od sebe učíme, je to lidské, nic lidského mi není cizí ... ;)
Offline
- (téma jako vyřešené označil(a) calis)
#3 05. 01. 2011 13:52 — Editoval jelena (05. 01. 2011 13:52)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická rovnice
Zdravím Vás, poslední řádek úprav není v pořádku (viz pravidla počítání s logaritmy (součin)) a také je zbytečný.
Lepší je na pravé straně nahradit 2 jako 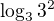 a odlogaritmovat levou a pravou stranu.
a odlogaritmovat levou a pravou stranu.
Nezapomenout na def. obor (argument log má být kladný).
Co označení témat - již se daří? (v 1. příspěvku tématu je takové tlačítko). Děkuji.
EDIT: omluva za dublicitní příspěvek.
Offline
#10 05. 01. 2011 15:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická rovnice
↑ calis: děkuji za označení témat :-)
↑ Cheop: děkuji za kompletní řešení pro kolegu. Jen drobnost - převod na log se základem 10, řekla bych, je operace navíc a trošku kolegu mate (jak pozoruji v tomto tématu).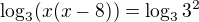
Zdravím.
Offline
#12 05. 01. 2011 17:13
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Logaritmická rovnice
↑ jelena:
Zdravím, já to dělám proto, že (ten převod)
nejdříve si vypočítám a pak píši.
A protože mám jen kalkulačku, která je součástí Windows
tak proto. Vím, že některé kalkulačky mají logaritmy o různých základech.
Nikdo není dokonalý
Offline
#13 05. 01. 2011 17:21
Re: Logaritmická rovnice
↑ Cheop: já mám kalkulačku o stejných základech ale neni mezi tím rozdíl , zda na ní píši ten či onen.... takze stejne píši klasicky
log 2 / log3 ...
Všichni se v něčem předstihujeme, proto se od sebe učíme, je to lidské, nic lidského mi není cizí ... ;)
Offline
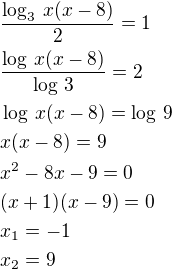
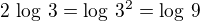
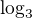 ale
ale 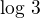 - opraveno
- opraveno