Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 04. 2008 15:08
- petulkacip
- Příspěvky: 38
- Reputace: 0
logaritmicka narovnice
prosim o pomoc, nejak tomu nemuzu prijit na kloub
urcete vsechna x v oboru realnych cisel pro ktera plati
(log_1/2 x)^2 > 0
prosim o postup, dekuji moc....
Offline
#7 05. 05. 2008 18:03
Re: logaritmicka narovnice
↑ Petra11:
Musis se poradne podivat, co se pocita. Hledame takova x, pro nez plati  . Jak uz tu moji predchudci psali nejdrive stanovime jaka x muzeme vubec do vyrazu s logaritmem dosadit...tim se omezime jen na
. Jak uz tu moji predchudci psali nejdrive stanovime jaka x muzeme vubec do vyrazu s logaritmem dosadit...tim se omezime jen na  .
.
Ted samotne reseni..protoze umocnujeme na druhou, je jasne, ze vyraz  je VZDY nezaporny, tzn.
je VZDY nezaporny, tzn.  . Ale my mame zjistit, kdy je JEN VETSI nez nula, takze to otocime...najdeme body, kdy je roven nule a ty ze vsech cisel, ktera muzeme do vyrazu dosadit vyloucime. Takze vlastne chceme, aby
. Ale my mame zjistit, kdy je JEN VETSI nez nula, takze to otocime...najdeme body, kdy je roven nule a ty ze vsech cisel, ktera muzeme do vyrazu dosadit vyloucime. Takze vlastne chceme, aby odmocnime
odmocnime .
.
Pro vsechny logaritmy plati, ze jsou rovny nule, pokud je jejich argument (vyraz za logaritmem) roven 1, takze odtud hned plyne 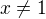 .
.
Shrnuti:
Ze vsech cisel, pro ktere zadany vyraz existuje, tj.  vyloucime hodnotu
vyloucime hodnotu 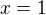 , proto ty kulate zavorky a vysledek ve tvaru
, proto ty kulate zavorky a vysledek ve tvaru  .
.
Offline
 . Najdi si definiční obor a vyřeš podmínku.
. Najdi si definiční obor a vyřeš podmínku.
 .
.