Matematické Fórum

Saturday

Pro pozitivně definitní matici A (http://cs.wikipedia.org/wiki/Pozitivn%C … %AD_matice) definujeme předpis: $<x|y> = x^T \cdot A \cdot y$ jako skalární součin na $R^n$

Je třeba ověřit axiomy:

První tři jsou jednoduché, potřebuju však vědět, jestli jsem správně ověřil ten poslední axiom, kterým je: $\forall x,y \in V: <x|y> = <y|x>$

Můj pokus
=====================

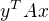$<x|y> = x^T A y = x^T A^T y = x^T A^T y = (x^T A^T) y = (A x)^T y = (A x)^T (y^T)^T = (y^T A x)^T = (y^T A x) = <y|x>$ - předposlední rovnost platí proto, že výsledkem $y^T A x$ je reálné číslo

Díky za pomoc :-)

btw: pokud by někdo měl odkaz, ve kterém se o dané problematice mluví, tak rozhodně nepohrdnu :-)

nika.v · 05. 05. 2008 11:21 — Editoval nika.v (05. 05. 2008 11:22)

↑ Saturday:

Ahojky, heleď já ti nevím, ale přijde mi, že tam máš trochu chaotický přehazování. My jsme tohle kdysi dávno dělali v Peanově aritmetice, tak si ji zkus najít na netu, bylo to při dokazování jeho axiomů. Zkusím ti napsat svůj postup od kroku č. 5, ale nevěř mi ani pozdrav :-D.pa eja

$(A*x)^T *y=(A*x*y^T)^T =(y^T *x*A)^T = y*(x*A)^T = y*(A*x)^T =$
$= y*x^T * A^T = y^T *x*A=<y/x>$

Saturday · 05. 05. 2008 13:16

↑ nika.v: Používám hlavne vlastnost 3 z http://en.wikipedia.org/wiki/Transpose#Properties .. Co ti prijde chaoticke, jaka cast?

Řekl bych, že hned ta první rovnost neplatí, protože když se podíváš na ten odkaz z Wiki, tak tam je uvedeno, že transpozice dvou matic je transpozice jednotlivych matic v opacnem poradi.

nika.v · 05. 05. 2008 13:43

↑ Saturday:

Ahojky,
aha, bych si taky musela pořádně přečíst zadání. Promiň matu tělem :-).

Saturday · 05. 05. 2008 18:45

↑ nika.v: :-)

Věděl by tedy někdo?

robert.marik

$(A x)^T y = (x A)^T (y^T)^T$

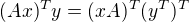
překlep? nebo kontrola jestli nejsme nepozorni? :)

ale jinak se mi to líbí

Saturday · 05. 05. 2008 19:27

↑ robert.marik: opravdu preklep :-) Diky

robert.marik

jina varianta:

Editace: tak nic, smazal jsem to, ono to bylo stejne dlouhe jako ten dukaz z dotazu

Saturday · 05. 05. 2008 19:31

Jasne, je to lepsi v tom, ze se nemusi nic rikat o souctu, jako jsem to musel delat ja.

robert.marik · 05. 05. 2008 19:38

\bibitem{www} I. Tammeraid et al., \textit{Applications of Linear Algebra},
\url{http://www.cs.ut.ee/~toomas_l/linalg/}

tohle byl pekny material a byly tam dukazy opravdu an urovni, ne tak jak to bava v materialech na webu.
odkaz uz nefunguje, ale treba to jenom presunuli a pujde to dohledat na webu podle jmen.

Saturday · 05. 05. 2008 21:39

↑ robert.marik: Bohužel jsem ten materiál nenašel, koukal jsem na tu stránku do kontaktů, ale ani mail jsem nenašel, takže se není jak dotázat.. škoda

robert.marik · 05. 05. 2008 22:52

To je skoda, byly tam opravdu peclive dukazy, tak jak to byva v "normalnich" knihach. Bylo to tak peclive napsane, ze jsem se nemusel bat je ocitovat v jednom svem clanku (z tama jsem taky kopiroval ten odkaz). Proste skoro jako normalni monografie. Kdyz si s tim dali tolik prace, tak to urcite je nekde vystavene nebo zrcadlene, jenom by chtelo zjistit kde .... Anebo ze by na to nekdo koupil autorka prava, chce to vydat a stahlo se to?
Ja jsem se po tom taky chvili pidil a taky zatim nic :(

Mozna mam par stranek vytistenych v praci, tak se zitra kouknu jestli tam neni napsane, kdo se skryva za tim "et. al" a treba se to bude dat dohledat podle jmen spoluautoru.

Matematické Fórum

#1 05. 05. 2008 00:53 — Editoval Saturday (05. 05. 2008 19:26)

Pozitivně definitní matice - skalární součin

#2 05. 05. 2008 11:21 — Editoval nika.v (05. 05. 2008 11:22)

Re: Pozitivně definitní matice - skalární součin

#3 05. 05. 2008 13:16

Re: Pozitivně definitní matice - skalární součin

#4 05. 05. 2008 13:43

Re: Pozitivně definitní matice - skalární součin

#5 05. 05. 2008 18:45

Re: Pozitivně definitní matice - skalární součin

#6 05. 05. 2008 19:23 — Editoval robert.marik (05. 05. 2008 19:24)

Re: Pozitivně definitní matice - skalární součin

#7 05. 05. 2008 19:27

Re: Pozitivně definitní matice - skalární součin

#8 05. 05. 2008 19:29 — Editoval robert.marik (05. 05. 2008 19:31)

Re: Pozitivně definitní matice - skalární součin

#9 05. 05. 2008 19:31

Re: Pozitivně definitní matice - skalární součin

#10 05. 05. 2008 19:38

Re: Pozitivně definitní matice - skalární součin

#11 05. 05. 2008 21:39

Re: Pozitivně definitní matice - skalární součin

#12 05. 05. 2008 22:52

Re: Pozitivně definitní matice - skalární součin

Zápatí