Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 05. 2008 23:25 — Editoval Jorica (05. 05. 2008 23:29)
#3 05. 05. 2008 23:28
Re: podmienka logaritmickej rovnice
↑ soyda21:
Na tvuj dotaz co s tim je pomerne jednoducha odpoved. Jak sam pises, mas zlomek, ktery ma byt vetsi nez nula.....a to je kdy?
1. citatel i jmenovat je kladny ... vysetris jako prunik intervalu
2. citatel i jmenovatel je zaporny ... opet prunik intervalu.
Vysledkem nude sjednoceni intervalu, ktere jsou vysledkem 1. a 2.
Offline
#5 05. 05. 2008 23:58
Re: podmienka logaritmickej rovnice
↑ soyda21:
Je to lomena fce.....mas pravdu, ze graficky ti to musi vyjit taky...ale me osobne by se nechtelo upravovat tvar te funkce do podoby, kdy ji nakreslim, kdyz staci vyresit 4 jednoduche nerovnice ;-)
Obema zpusoby vyjde 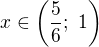
Offline

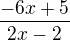 ma by? väčšie ako nula, ale nejako neviem čo s tým, v podstate je to lineárna lomená funcia?
ma by? väčšie ako nula, ale nejako neviem čo s tým, v podstate je to lineárna lomená funcia?